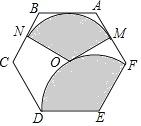
【题目】如图，点O为正六边形ABCDEF的中心，点M为AF中点，以点O为圆心，以OM的长为半径画弧得到扇形MON，点N在BC上；以点E为圆心，以DE的长为半径画弧得到扇形DEF，把扇形MON的两条半径OM，ON重合，围成圆锥，将此圆锥的底面半径记为r1；将扇形DEF以同样方法围成的圆锥的底面半径记为r2，则r1：r2=_____．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】在△ABC中，D、E分别是边AB、BC上的点，AE和CD交于点F，且∠CFE＝∠B。
（1）如图1，求证：∠AEC＝∠CDB；
（2）如图2，过点C作CG⊥AC，交AB于点G，CD⊥CB，∠ACD ＝∠CAB－∠B，求证：AC＝GC；
（3）如图3，在（2）的条件下，CE＋CD＝AE，CG＝
，求线段BC的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，已知点B的坐标为（6，4）．
（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）
（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．
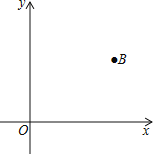
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知港口A东偏南10°方向有一处小岛B，一艘货轮从港口A沿南偏东40°航线出发，行驶80海里到达C处，此时观测小岛B在北偏东60°方向．
（1）求此时货轮到小岛B的距离．
（2）在小岛周围36海里范围内是暗礁区，此时轮船向正东方向航行有没有触礁危险？请作出判断并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（3分）以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a，b互相平行的是（ ）
A. 如图1，展开后测得∠1=∠2
B. 如图2，展开后测得∠1=∠2且∠3=∠4
C. 如图3，测得∠1=∠2
D. 如图4，展开后再沿CD折叠，两条折痕的交点为O，测得OA=OB，OC=OD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 推理填空
已知：如图所示，点B，C，E在同一条直线上，AB∥CD，∠1=∠2，∠3=∠4，求证：AD∥BE
证明：∵AB∥CD（已知）
∴∠4=∠______（______）
∵∠3=∠4（已知）∴∠3=∠______（______）
∴∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF（等式的性质）
即∠BAF=∠DAC
∴∠3=∠______（等量代换）
∴AD∥BE（______）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC中，∠BAC=100°．
（1）若∠ABC和∠ACB的角平分线交于点O，如图1所示，试求∠BOC的大小；
（2）若∠ABC和∠ACB的三等分线（即将一个角平均分成三等分的射线）相交于O，O1，如图2所示，试求∠BOC的大小；
（3）如此类推，若∠ABC和∠ACB的n等分线自下而上依次相交于O，O1，O2…，如图3所示，试探求∠BOC的大小与n的关系，并判断当∠BOC=170°时，是几等分线的交线所成的角．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
