练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，为了估算河的宽度，我们可以在河对岸选定一个目标点A，再在河岸的这一边选取点B和点C，使AB⊥BC，然后再选取点E，使EC⊥BC，用视线确定BC和AE的交点D，此时如果测得BD=160m，DC=80m，EC=50m，求A、B间的大致距离．

    分析 根据题意得出△ABD∽△ECD，进而利用相似三角形的性质得出AB的长．

    解答 解：由题意可得：∠ABD=∠ECD=90°，∠ADB=∠EDC，
    则△ABD∽△ECD，
    故$\frac{BD}{DC}$=$\frac{AB}{EC}$，
    即$\frac{160}{80}$=$\frac{AB}{50}$，
    解得：AB=100．
    答：A、B间的距离为100m．

    点评 此题主要考查了相似三角形的应用，根据题意得出相似三角形是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．计算：（$\sqrt{5}$+2）2015•（$\sqrt{5}$-2）2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

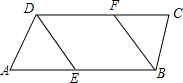    2．如图，已知∠ABC=∠ADC，BF、DE分别平分∠ABC，∠ADC，且∠AED=∠ABF，求证：∠A=∠C．
    证明：∵BF，DE分别平分∠ABC，∠ADC（已知）
    ∴∠ABF=$\frac{1}{2}$∠ABC，∠CDE=$\frac{1}{2}$∠ADC（角平分线的定义）
    ∵∠ABC=∠ADC=（已知）
    ∴∠ABF=∠CDE（等式的性质）
    ∵∠AED=∠ABF（已知）
    ∴∠AED=∠CDE（等量代换）
    ∴AB∥CD（内错角相等，两直线平行）
    ∴∠A+∠ADC=180°，∠C+∠ABC=180°（两直线平行，同旁内角互补）
    ∵∠ABC=∠ADC（已知）
    ∴∠A=∠C（等式的性质）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

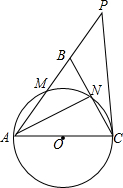    19．如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．
    （1）求证：直线CP是⊙O的切线；
    （2）若BC=2$\sqrt{5}$，sin∠BCP=$\frac{\sqrt{5}}{5}$，求点B到AC的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．若三角形面积为18，内切圆的半径3，则该三角形的周长为12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．“$\frac{16}{49}$的平方根是±$\frac{4}{7}$”用数学式表示为（　　）
    A．$\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$B．$\sqrt{\frac{16}{49}}$=$\frac{4}{7}$C．±$\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$D．-$\sqrt{\frac{16}{49}}$=-$\frac{4}{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．$\sqrt{（-8）^{2}}$=8，（$\sqrt{8}$）2=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：
    （1）-$\root{3}{2\frac{10}{27}}$                 
    （2）$\root{3}{1-\frac{37}{64}}$
    （3）$\root{3}{-27}$+$\sqrt{（-3）^{2}}$-$\root{3}{-1}$           
    （4）$\sqrt{0.04}$+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

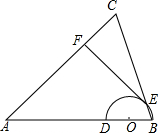    1．已知：如图，在△ABC中，AB=AC，点O在边AB上，半圆O过点B，且分别与边AB、BC交于点D、E，点D与点A不重合，EF⊥AC，垂足为F．
    （1）求证：直线EF是半圆O的切线；
    （2）若FC=3，BE=2，OB=2，求BC的长．

    查看答案和解析>>

    同步练习册答案