Question

【题目】如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ．

（1）如图a，求证：△BCP≌△DCQ；
（2）如图，延长BP交直线DQ于点E．
①如图b，求证：BE⊥DQ；
②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．

Answer 1

【答案】
（1）证明：∵∠BCD=90°，∠PCQ=90°，

∴∠BCP=∠DCQ，

在△BCP和△DCQ中，

，

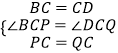∴△BCP≌△DCQ

（2）解：①如图b，∵△BCP≌△DCQ，

∴∠CBF=∠EDF，又∠BFC=∠DFE，

∴∠DEF=∠BCF=90°，

∴BE⊥DQ；

②∵△BCP为等边三角形，

∴∠BCP=60°，∴∠PCD=30°，又CP=CD，

∴∠CPD=∠CDP=75°，又∠BPC=60°，∠CDQ=60°，

∴∠EPD=45°，∠EDP=45°，

∴△DEP为等腰直角三角形．

【解析】（1）根据旋转的性质证明∠BCP=∠DCQ，得到△BCP≌△DCQ；（2）①根据全等的性质和对顶角相等即可得到答案；

②根据等边三角形的性质和旋转的性质求出∠EPD=45°，∠EDP=45°，判断△DEP的形状．

【考点精析】解答此题的关键在于理解旋转的性质的相关知识，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．