
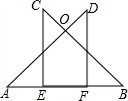
 如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.
如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD. 分析 先求出AF=BE,再利用“角边角”证明△ADF和△BCE全等,根据全等三角形对应边相等可得AD=BC,再根据等角对等边求出AO=BO,然后证明即可.
解答 证明:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
∵CE⊥AB,DF⊥AB,
∴∠AFD=∠BEC=90°
在△ADF和△BCE中,$\left\{\begin{array}{l}{∠A=∠B}\\{AF=BE}\\{∠AFD=∠BEC=90°}\end{array}\right.$,
∴△ADF≌△BCE(ASA),
∴AD=BC,
∵∠A=∠B,
∴AO=BO,
∴BC-BO=AD-AO,
即OC=OD.
点评 本题考查了全等三角形的判定与性质,等角对等边的性质,熟练掌握三角形全等的判断方法并准确确定出全等三角形是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.
如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
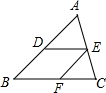 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com