
分析 由向量$\overrightarrow{a}$=(-1,3),$\overrightarrow{b}$=(1,t),可求得$\overrightarrow{a}$-2$\overrightarrow{b}$,然后由($\overrightarrow{a}$-2$\overrightarrow{b}$)⊥$\overrightarrow{a}$,根据垂直向量的关系,可得($\overrightarrow{a}$-2$\overrightarrow{b}$)•$\overrightarrow{a}$=$\overrightarrow{0}$,继而求得t的值,则可求得答案.
解答 解:∵向量$\overrightarrow{a}$=(-1,3),$\overrightarrow{b}$=(1,t),
∴$\overrightarrow{a}$-2$\overrightarrow{b}$=(-3,3-2t),
∵($\overrightarrow{a}$-2$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$-2$\overrightarrow{b}$)•$\overrightarrow{a}$=$\overrightarrow{0}$,
∴3+3(3-2t)=0,
解得:t=2,
∴$\overrightarrow{b}$=(1,2),
∴|$\overrightarrow{b}$|=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题考查了平面向量的知识.注意理解垂直向量的关系是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
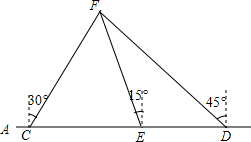 如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.
如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
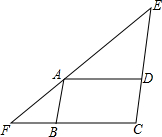 如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.
如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com