
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证: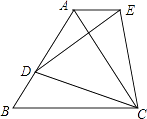
(1)△AEC≌BDC;
(2)AE∥BC.
【答案】
(1)证明:∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠BCA=∠ECD=60°,∠B=60°,
∴∠BCA﹣∠DCA=∠ECD﹣∠DCA,
即∠BCD=∠ACE,
在△AEC和△BDC中,
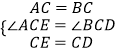 ,
,
∴△AEC≌△BDC(SAS)
(2)证明:∵△AEC≌△BDC,
∴∠EAC=∠B,
∵∠B=60°,
∴∠EAC=∠B=60°=∠ACB,
∴AE∥BC
【解析】(1)由△ABC和△DEC是等边三角形,得到三边相等,三角都是60°,再根据SAS得到△AEC≌△BDC;(2)由(1)中的△AEC≌△BDC,得到对应角相等,再根据内错角相等两直线平行,得到AE∥BC.
【考点精析】根据题目的已知条件,利用平行线的判定的相关知识可以得到问题的答案,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )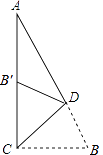
A.25°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?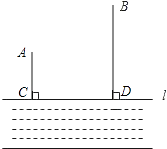
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一项工程预计在规定的日期内完成,如果甲独做刚好能完成,如果乙独做就要超过日期3天,现在甲、乙两人合做2天,剩下的工程由乙独做,刚刚好在规定的日期完成,问规定日期是几天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com