
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )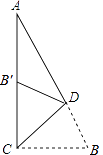
A.25°
B.30°
C.35°
D.40°
【答案】D
【解析】解:∵在Rt△ACB中,∠ACB=90°,∠A=25°,
∴∠B=90°﹣25°=65°,
∵△CDB′由△CDB反折而成,
∴∠CB′D=∠B=65°,
∵∠CB′D是△AB′D的外角,
∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°.
所以答案是:D.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一个边长为2个单位长度的等边△ABC,满足AC∥y轴.平移△ABC得到△A′B′C′,使点A′、B′分别在x轴、y轴上(不包括原点),则此时点C′的坐标是..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料并回答问题:
在解分式方程 ![]() 时,小明的解法如下:
时,小明的解法如下:
解:方程两边同乘以(x+1)(x﹣1),得2(x﹣1)﹣3=1①
去括号,得2x﹣1=3﹣1 ②
解得x= ![]()
检验:当x= ![]() 时,(x+1)(x﹣1)≠0 ③
时,(x+1)(x﹣1)≠0 ③
所以x= ![]() 是原分式方程的解 ④
是原分式方程的解 ④
(1)你认为小明在哪里出现了错误(只填序号)
(2)针对小明解分式方程出现的错误和解分式方程中的其他重要步骤,请你提出三条解分式方程时的注意事项;
(3)写出上述分式方程的正确解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)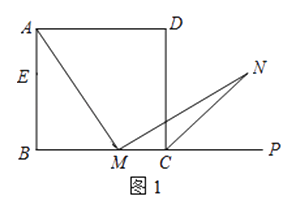
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.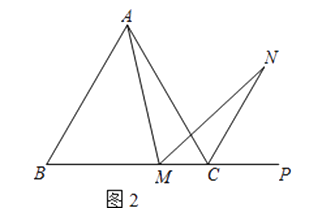
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证: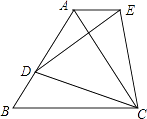
(1)△AEC≌BDC;
(2)AE∥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com