
【题目】综合题
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)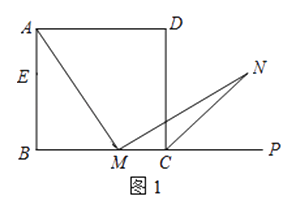
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.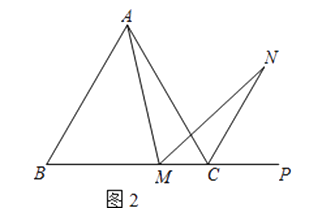
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
【答案】
(1)证明:在边AB上截取AE=MC,连接ME.
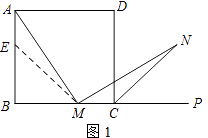
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=45°,∴∠AEM=135°.
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,∴∠MCN=135°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN
(2)解:结论AM=MN还成立
证明:在边AB上截取AE=MC,连接ME.
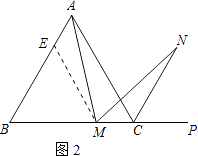
在正△ABC中,∠B=∠BCA=60°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=60°,∴∠AEM=120°.
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,∴∠MCN=120°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN
(3)解:若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则当∠AMN= ![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.
【解析】(1)根据正方形的性质四边相等,四角都是90°,得到△AEM≌△MCN,根据全等三角形的对应边相等,得到AM=MN;(2)根据正三角形的性质三个角都是60°,三边相等,得到△AEM≌△MCN,得到AM=MN;(3)根据规律得到当∠AMN=(n2)·180°÷n时,结论AM=MN仍然成立.


科目:初中数学 来源: 题型:
【题目】如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )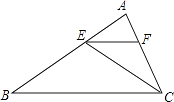
A.64°
B.32°
C.36
D.26°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )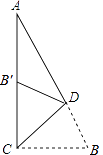
A.25°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
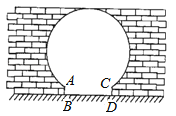
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2018年庆阳市大约有24406人参加中考,将数据24406用科学记数法表示为( )
A. 2.4406×103B. 2.4406×104C. 2.4406×103D. 24.406×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?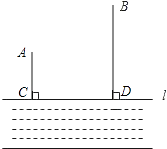
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com