
【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 与
与![]() 相交于点
相交于点![]() .
.
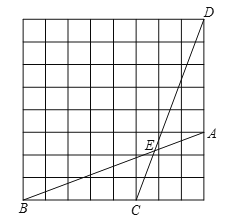
(1)![]() 的长等于 ;
的长等于 ;
(2)![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,满足
,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点
,请在如图所示的网格中,用无刻度的直尺,画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明) .
的位置是如何找到的(不要求证明) .
【答案】(1)![]() ;(2)图见解析;取格点G、H,连接GH与CD 相交于点 F,连接 BF,BD,取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,点 P即为所求.
;(2)图见解析;取格点G、H,连接GH与CD 相交于点 F,连接 BF,BD,取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,点 P即为所求.
【解析】
(1)根据勾股定理计算即可;
(2)求出![]() ,然后作出DF=EC,可得
,然后作出DF=EC,可得![]() ,即可得到点F,然后取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,作FM∥EK,根据平行线分线段成比例定理求出
,即可得到点F,然后取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,作FM∥EK,根据平行线分线段成比例定理求出![]() ,进而得到
,进而得到![]() ,再利用平行线分线段成比例定理即可得到
,再利用平行线分线段成比例定理即可得到![]() ,故点 P为所求.
,故点 P为所求.
解:(1)由勾股定理得:CD![]() ;
;
(2)如图,取格点G、H,连接GH与CD 相交于点 F,连接 BF,BD,取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,点 P即为所求.
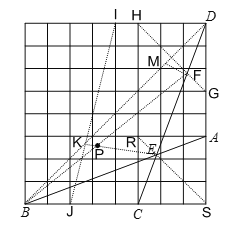
证明:如图,由图易得EA=EC,
∴点E在直线RS上,
∵RC∥DS,且![]() ,
,
∴![]() ,
,
取格点G、H,连接GH与CD 相交于点 F,则DF=EC,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
取格点 I、J,连接 IJ 与 BD交于点 K,连接EK与 BF交于点P,
∵BS∥ID,![]() ,
,
∴![]() ,
,
作FM∥EK,则![]() ,
,
∴设BK=4a,则DK=8a,DM=3a,MK=5a,
∴![]() ,
,
∵FM∥EK,
∴![]() .
.


科目:初中数学 来源: 题型:
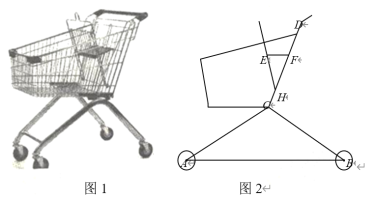
【题目】如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为5 cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm.
(1)求扶手前端D到地面的距离;
(2)手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10 cm,DF=20cm,EF∥AB,∠EHD=45°,求坐板EF的宽度.(本题答案均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列说法,错误的个数是( )
①![]() 是分式;②当x≠1时,
是分式;②当x≠1时,![]() 成立;③当x=﹣3时,分式
成立;③当x=﹣3时,分式![]() 的值是零;④a
的值是零;④a![]() ;⑤
;⑤![]() ;⑥2﹣x
;⑥2﹣x![]() .
.
A.6个B.5个C.4个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() ,sin64°≈
,sin64°≈![]() ,tan64°≈2)
,tan64°≈2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]()
![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)已知点![]() (4,2),将抛物线
(4,2),将抛物线![]() 向上平移得抛物线
向上平移得抛物线![]() ,点
,点![]() 平移后的对应点为
平移后的对应点为![]() ,且
,且![]() ,求抛物线
,求抛物线![]() 的解析式;
的解析式;
(3)将抛物线![]() :
:![]() 沿
沿![]() 轴翻折,得抛物线
轴翻折,得抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ),与直线
),与直线![]() 交于点
交于点![]() (
(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
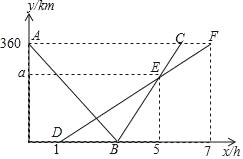
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
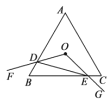
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com