
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形). 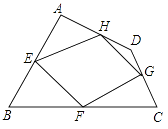
(1)四边形EFGH的形状是 , 证明你的结论;
(2)当四边形ABCD的对角线满足条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
【答案】
(1)平行四边形
(2)互相垂直
(3)菱形
【解析】解:(1.)四边形EFGH的形状是平行四边形.理由如下: 如图,连结BD.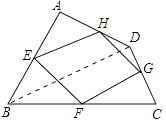
∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2.)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连结AC、BD.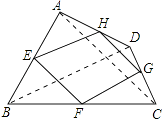
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
(3.)菱形的中点四边形是矩形.理由如下:
如图,连结AC、BD.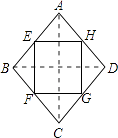
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH= ![]() BD,FG=
BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.
故答案为:平行四边形;互相垂直;菱形.
(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH= ![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═ ![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答.
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答.


科目:初中数学 来源: 题型:
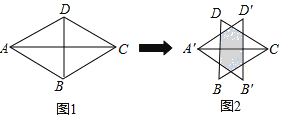
【题目】 如图,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图2,则阴影部分的周长为( )
A.1 B.2 C.2.5 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ACB=90°,点D,E分别为AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证:四边形DECF为平行四边形. 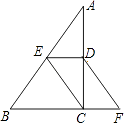
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列语句:
①邻补角的平分线互相垂直;②互补的两个角一定是一个为锐角,另一个为钝角;③延长线段AO到C,使OC=OA;④这个角等于30°吗?在这些语句中,属于真命题的是_______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
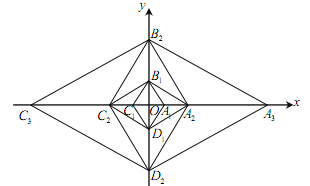
【题目】(成都)已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com