
如图,B、C、E 三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE 若∠A=40°,求∠BCD 的度数.
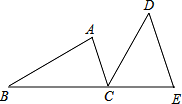
【考点】全等三角形的判定与性质.
【分析】(1)根据平行线的性质可得∠ACB=∠DEC,∠ACD=∠D,再由∠ACD=∠B 可得∠D=∠B, 然后可利用 AAS 证明△ABC≌△CDE,进而得到 CB=DE;
根据全等三角形的性质可得∠A=∠DCE=40°,然后根据邻补角的性质进行计算即可.
【解答】(1)证明:∵AC∥DE,
∴∠ACB=∠DEC,∠ACD=∠D,
∵∠ACD=∠B.
∴∠D=∠B,
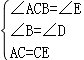 在△ABC 和△DEC 中,
在△ABC 和△DEC 中,
,
∴△ABC≌△CDE(AAS),
∴CB=DE;
解:∵△ABC≌△CDE,
∴∠A=∠DCE=40°
∴∠BCD=180°﹣40°=140°.
【点评】此题主要考查了全等三角形的性质和判定,关键是掌握全等三角形的性质证明线段和角相 等的重要工具.


科目:初中数学 来源: 题型:
已知正比例函数 y1=k1x 的图象与一次函数 y2=k2x﹣9 的图象交于点 P(3,﹣6).
(1)求 k1、k2 的值;
根据函数图象直接写出 y2<y1<0 时,自变量 x 的取值范围;
(3)这两个函数图象与 y 轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
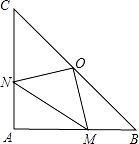
如图,在△ABC 中,∠A=90°,AB=AC,O 是 BC 的中点,如果在 AB 和 AC 上分别有一个动 点 M、N 在移动,且在移动时保持 AN=BM.
(1)请你判断△OMN 的形状,并说明理由. 若 BC=2 ,则 MN 的最小值为 .
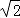
查看答案和解析>>
科目:初中数学 来源: 题型:
某校在“校园十佳歌手”比赛上,六位评委给1号选手的评分如下:90,96,91,96,95,94.那么,这组数据的众数和中位数分别是( )
A.96,94.5 B.96,95
C.95,94.5 D.95,95
查看答案和解析>>
科目:初中数学 来源: 题型:
已知两点M(3,2),N(-1, 3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为
A. (0,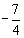 ) B. (
) B. (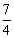 ,0) C. (
,0) C. (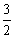 ,0) D. (
,0) D. (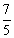 ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com