
| 销售方式 | 直接销售 | 加工成半成品 | 加工成成品 |
| 每方米获利(元) | 100 | 250 | 450 |
分析 (1)设该厂加工成品x天,则加工半成品为(10-x)天,根据“该厂计划在10天内刚好加工完140立方米木材”列出方程并解答;
(2)设至少将a立方米木材进行加工成品,则(140-a)立方米木材进行加工半成品,根据获利不能少于42200元,列出不等式,进一步分析探讨的出答案即可.
解答 解:(1)设该厂加工成品x天,则加工半成品为(10-x)天,
依题意得:6x+16(10-x)=140,
解得x=2,
则10-x=10-2=8(天).
答:该厂加工成品2天,则加工半成品为8天;
(2)设至少将a立方米木材进行加工成品,则(140-a)立方米木材进行加工半成品,由题意得
450a+250(140-a)≥42200
解得:a≥36,
则36÷6+(140-36)÷16=13.5天.
答:该厂要加工这140立方米的木材需要13.5天.
点评 本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,找到关键描述语,理解公司获利的计算方法列出方程和不等式.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
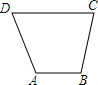 为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.
为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10h | B. | $\frac{1}{6}$h | C. | $\frac{80}{13}$h | D. | 6h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
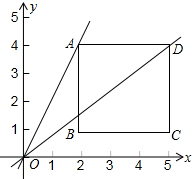 如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).
如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com