
����Ŀ����ͼ��һ��Բ����ˮ�ص����봹ֱ��ˮ�氲װ��һ��������ˮװ��OA��Oǡ����ˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�����ͼ��ʾ����ֱ������ϵ��ˮ������ĸ߶�y(m)��ˮƽ����x(m)֮��Ĺ�ϵʽ������y����x2+bx+c��ʾ���������߾�����B(![]() ��2)��C(2��
��2)��C(2��![]() )�������������Ϣ������������⣻
)�������������Ϣ������������⣻
(1)�������ߵĺ�����ϵʽ����ȷ����ˮװ��OA�ĸ߶ȣ�
(2)�����ˮ����ˮ������߶��Ƕ����ף�
(3)�������������أ�ˮ�صİ뾶����Ҫ�����ף�����ʹ�����ˮ�����������ڳ��⣿

���𰸡�(1)y����x2+2x+![]() ����ˮװ��OA�ĸ߶���
����ˮװ��OA�ĸ߶���![]() �ף�(2)�����ˮ����ˮ������߶���
�ף�(2)�����ˮ����ˮ������߶���![]() �ף�(3)ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮
�ף�(3)ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮
��������
(1)���ݴ���ϵ������ֻ�轫B��C���������κ�������ʽ����������κ����Ľ���ʽ��
(2)���������ߵĶ��㣬����������ˮ������ˮ������߶ȣ�
(3)��������ֻ���ҵ���������x�ύ��ĺ����꣬����������ˮ������Զ���룬���ɵó���.
�⣺(1)��������y����x2+bx+c��ʾ���Ҿ�����B(![]() ��2)��C(2��
��2)��C(2��![]() )��
)��
��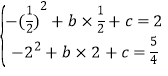 ��
��
��ã�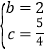 ��
��
��������y����x2+2x+![]() ��
��
��x��0ʱ��y��![]() ��
��
�������ߵĺ�����ϵʽ��y����x2+2x+![]() ����ˮװ��OA�ĸ߶���
����ˮװ��OA�ĸ߶���![]() �ף�
�ף�
(2)��y����x2+2x+![]() ����(x��1)2+
����(x��1)2+![]() ��
��
�൱x��1ʱ��yȡ�����ֵ����ʱy��![]() ��
��
�������ˮ����ˮ������߶���![]() �ף�
�ף�
(3)�x2+2x+![]() ��0��
��0��
��ã�x1����0.5��x2��2.5��
��ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
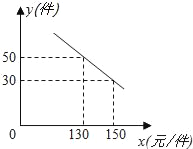
����Ŀ��ij�̳�����һ��ÿ���۸�Ϊ100Ԫ������Ʒ�����̳��������֣����۵���x��Ԫ/������ÿ��������y������֮��������ͼ��ʾ�Ĺ�ϵ����1�����y��x֮��ĺ�����ϵʽ����2������̵�����������Ʒ��ÿ��Ҫ���1500Ԫ������ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ����3��д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ���������̳������ˣ��Ὣ�ۼ۶�Ϊ���٣�����֤ÿ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
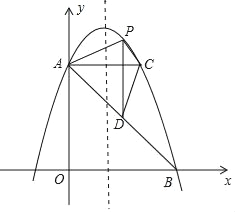
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����x+5��y�ύ�ڵ�A����x�ύ�ڵ�B��������y����x2+bx+c��A��B���㣮
��1��д����A��B�����ꣻ
��2���������ߵĽ���ʽ��
��3������A��ACƽ����x�ᣬ���������ڵ�C����PΪ�������ϵ�һ���㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D���ʵ���P�ں�λ��ʱ���ı���APCD�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ����ԭ��һ��¥����֣�ݻ�չ����(�׳ơ������ס�)�����ڷ羰�续�������������֣�ݹ۹���ο���Ӱ����Ѿ��㣮ѧ�������Ǻ���֪ʶ������������ͬѧ�������Լ�ѧ����֪ʶ�����������ס��ĸ߶ȣ������ƶ��˲��������������ÿ���ʱ�������ʵ�ز�����������Ŀ��������±���
��Ŀ | ���� | |||
���� | ����֣�ݻ�չ���ݵĸ߶� | |||
����ʾ��ͼ |
| ��ͼ����E���ò�����DE���¥��B������������ǰ��һ�ξ��뵽��C���ò�����CF���¥��B�������������ҵ�A��B��C��D��E��F����ͬһ��ֱƽ���� | ||
�������� | �����Ķ��� | �����Ķ��� | EC�ij��� | ������DE��CF�ĸ߶� |
40�� | 45�� | 53�� | 1.5�� | |
�� | �� | |||
���������С������ϱ��еIJ������ݣ����֣�ݻ�չ���ݵĸ߶�(�ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84�������������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
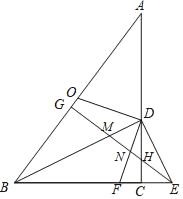
����Ŀ���ڡ�ABC�У���ACB��90�㣬BC��3��AC��4����O��AB���е㣬��D�DZ�AC��һ�㣬DE��BD����BC���ӳ����ڵ�E��OD��DF����BC���ڵ�F������E��EG��AB������Ϊ��G��EG�ֱ�BD��DF��DC�ڵ�M��N��H��
(1)��֤��![]() ��
��
(2)��CD��x��NE��y����y����x�ĺ�����ϵʽ���䶨����
(3)����DEF����DEΪ���ĵ���������ʱ�����߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
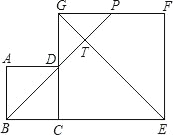
����Ŀ����ͼ���߳��ֱ�Ϊ4��8������������ABCD��CEFG���ŷ���һ������BD���ӳ���EG�ڵ�T����FG�ڵ�P����GT�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��3x��0��
�⣺��x2��3x��0����ã�x1��0��x2��5����������y��x2��3x��x��Ľ�������Ϊ��0��0���ͣ�3��0�����������κ���y��x2��3x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0��x��3ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��3x��0�����ԣ�һԪ���β���ʽx2��3x��0�Ľ⼯Ϊ��x��0��x��3��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1�������������У�����������ѧ˼���е��� ������ ������ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼�� ������˼��
��2��һԪ���β���ʽx2��3x��0�Ľ⼯Ϊ�� ����
��3�������Ƶķ�����һԪ���β���ʽ��x2��3x��4��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
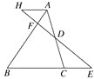
����Ŀ����ͼ����ABC�У�D��AC���е㣬E��BC�ӳ�����һ�㣬��A��AH��BE������ED���ӳ���AB��F����AH��H.
(1)��֤��AH��CE��
(2)���AB��4AF��EH��8����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϣ������Ѹ�ͷ�չ������ȥ�̳������֧����ʽ���Ӷ�������ݣ�ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��֧����ʽ���������������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ������������ǡ��ѡ��ͬһ��֧����ʽ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com