
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大王米”的高度,他们制订了测量方案,并利用课余时间完成了实地测量.测量项目及结果如下表:
项目 | 内容 | |||
课题 | 测量郑州会展宾馆的高度 | |||
测量示意图 |
| 如图,在E点用测倾器DE测得楼顶B的仰角是α,前进一段距离到达C点用测倾器CF测得楼顶B的仰角是β,且点A、B、C、D、E、F均在同一竖直平面内 | ||
测量数据 | ∠α的度数 | ∠β的度数 | EC的长度 | 测倾器DE,CF的高度 |
40° | 45° | 53米 | 1.5米 | |
… | … | |||
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的右端点运动到M点的时刻为0,用t(秒)表示l的运动时间.

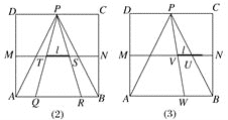
(1)请你针对图(1)(2)(3)中l位于不同位置的情形分别画出在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2;
②2≤t≤3;
③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
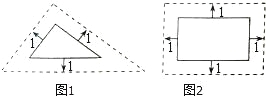
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
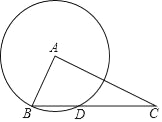
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
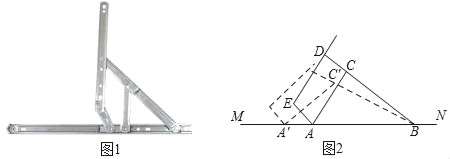
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CFCE=CDBC.
(1)求证:△ACF∽△ECA;
(2)当CE平分∠ACB时,求证:![]() =
=![]() .
.
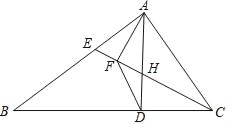
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=﹣x2+bx+c表示,且抛物线经过点B(![]() ,2),C(2,
,2),C(2,![]() ).请根据以上信息,解答下列问题;
).请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为__________.
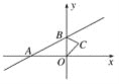
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3,根据图中数据完成填空,再按要求答题:sin2A1+sin2B1=____;sin2A2+sin2B2=____;sin2A3+sin2B3=____.
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=____;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理证明你的猜想;
(3)已知∠A+∠B=90°,且sinA=![]() ,求sinB的值.
,求sinB的值.
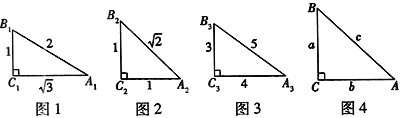
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com