
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
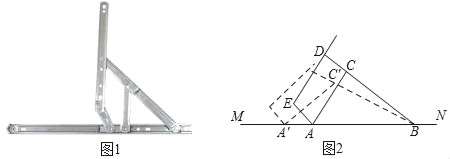
【答案】(1)支点D到滑轨MN的距离为23厘米;(2)滑块A向左侧移动的距离是6厘米.
【解析】
(1)过C作CG⊥AB于G,过D作DH⊥AB于H,解直角三角形顶点AG![]() AC=10,CG
AC=10,CG![]() AG=10
AG=10![]() ,根据相似三角形的性质得到DH;
,根据相似三角形的性质得到DH;
(2)过C'作C'S⊥MN于S,解直角三角形得到A'S=C'S=10![]() ,求得A'B=10
,求得A'B=10![]() 10
10![]() ,根据线段的和差即可得到结论.
,根据线段的和差即可得到结论.
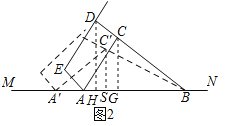
(1)过C作CG⊥AB于G,过D作DH⊥AB于H.
∵AC=20,∠CAB=60°,∴AG![]() AC=10,CG
AC=10,CG![]() AG=10
AG=10![]() .
.
∵BC=BD﹣CD=30,CG⊥AB,DH⊥AB,∴CG∥DH,∴△BCG∽△BDH,∴![]() ,∴
,∴![]() ,∴DH
,∴DH![]() 23(厘米);
23(厘米);
∴支点D到滑轨MN的距离为23厘米;
(2)过C'作C'S⊥MN于S.
∵A'C'=AC=20,∠C'A'S=45°,∴A'S=C'S=10![]() ,∴BS
,∴BS![]() 10
10![]() ,∴A'B=10
,∴A'B=10![]() 10
10![]() .
.
∵BG![]() 10
10![]() ,∴AB=10+10
,∴AB=10+10![]() ,∴AA'=A'B﹣AB≈6(厘米),∴滑块A向左侧移动的距离是6厘米.
,∴AA'=A'B﹣AB≈6(厘米),∴滑块A向左侧移动的距离是6厘米.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
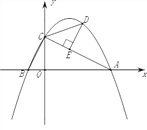
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
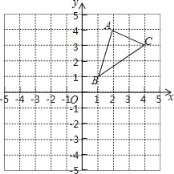
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;并写出A1、B1、C1三点的坐标.
(2)求出(1)中C点旋转到C1点所经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
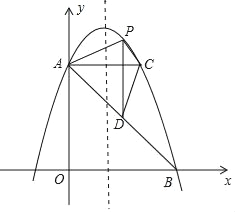
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与y轴交于点A,与x轴交于点B.抛物线y=﹣x2+bx+c过A、B两点.
(1)写出点A,B的坐标;
(2)求抛物线的解析式;
(3)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一动点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大王米”的高度,他们制订了测量方案,并利用课余时间完成了实地测量.测量项目及结果如下表:
项目 | 内容 | |||
课题 | 测量郑州会展宾馆的高度 | |||
测量示意图 |
| 如图,在E点用测倾器DE测得楼顶B的仰角是α,前进一段距离到达C点用测倾器CF测得楼顶B的仰角是β,且点A、B、C、D、E、F均在同一竖直平面内 | ||
测量数据 | ∠α的度数 | ∠β的度数 | EC的长度 | 测倾器DE,CF的高度 |
40° | 45° | 53米 | 1.5米 | |
… | … | |||
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
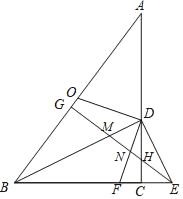
【题目】在△ABC中,∠ACB=90°,BC=3,AC=4,点O是AB的中点,点D是边AC上一点,DE⊥BD,交BC的延长线于点E,OD⊥DF,交BC边于点F,过点E作EG⊥AB,垂足为点G,EG分别交BD、DF、DC于点M、N、H.
(1)求证:![]() ;
;
(2)设CD=x,NE=y,求y关于x的函数关系式及其定义域;
(3)当△DEF是以DE为腰的等腰三角形时,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣3x>0.
解:设x2﹣3x=0,解得:x1=0,x2=5.则抛物线y=x2﹣3x与x轴的交点坐标为(0,0)和(3,0).画出二次函数y=x2﹣3x的大致图象(如图所示),由图象可知:当x<0或x>3时函数图象位于x轴上方,此时y>0,即x2﹣3x>0,所以,一元二次不等式x2﹣3x>0的解集为:x<0或x>3.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解答过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想 ④整体思想
(2)一元二次不等式x2﹣3x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣3x﹣4<0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
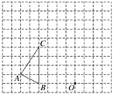
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)以O为位似中心,在点O的同侧作△A1B1C1,使得它与原三角形的位似比为1∶2;
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,并求出点A旋转的路径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com