
分析 (1)根据已知中二次根式的化简即可得出答案.
(2)利用(1)中计算结果,即可得出二次根式的变化规律,进而得出答案即可.
解答 解:(1)5$\sqrt{\frac{5}{24}}$=$\sqrt{5+\frac{5}{24}}$.
5$\sqrt{\frac{5}{24}}$
=$\sqrt{\frac{{5}^{3}}{24}}$,
=$\sqrt{\frac{{5}^{3}-5+5}{24}}$,
=$\sqrt{\frac{5{(5}^{2}-1)+5}{{5}^{2}-1}}$,
=$\sqrt{5+\frac{5}{{5}^{2}-1}}$,
=$\sqrt{5+\frac{5}{24}}$;
(2)n$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$(n为正整数,n≥2).
点评 此题主要考查了数字变化规律,根据已知得出根式内外变化规律是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y1=-x+1与双曲线y2=$\frac{k}{x}$ 交于A,B两点,过A作AC垂直于x轴,△ACO的面积为3,现有下面结论:①k=6;②当x>0时,y1>y2;③若B点坐标为(a,b),则$\sqrt{a+b}$=1;④若B点坐标为(a,b),则$\frac{b}{a}+\frac{a}{b}=-\frac{13}{6}$,其中正确的结论有③④(写出所有正确结论的序号即可).
如图,直线y1=-x+1与双曲线y2=$\frac{k}{x}$ 交于A,B两点,过A作AC垂直于x轴,△ACO的面积为3,现有下面结论:①k=6;②当x>0时,y1>y2;③若B点坐标为(a,b),则$\sqrt{a+b}$=1;④若B点坐标为(a,b),则$\frac{b}{a}+\frac{a}{b}=-\frac{13}{6}$,其中正确的结论有③④(写出所有正确结论的序号即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
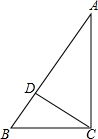 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com