
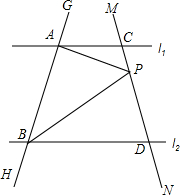
 已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).分析 (1)过P作PE∥AC,根据平行线的性质可得∠CAP=∠1,∠PBD=∠2,进而可得∠APB=∠CAP+∠PBD;
(2)根据题意作图,由平行线与外角的性质即可求得答案.
解答 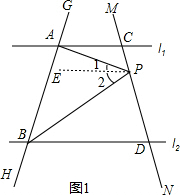 解:(1)如图1,过P作PE∥AC,
解:(1)如图1,过P作PE∥AC,
∵l1∥l2,
∴AC∥EP∥DB,
∴∠CAP=∠1,∠PBD=∠2,
∴∠APB=∠CAP+∠PBD;
(2)如图2,若点P在AC下方,
设PA交BD于点E,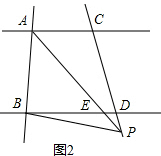 ∵AC∥BD,
∵AC∥BD,
∴∠PAC=∠PED,
∵∠PED=∠PBD+∠APB,
∴∠APB=∠PBD-∠PAC,
若点P在AC上方,则∠APB=∠PBD+∠PAC.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题

| A. | 14元 | B. | 15元 | C. | 16元 | D. | 17元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
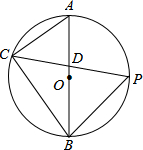 如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com