
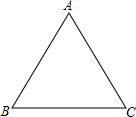
 如图,已知△ABC是等腰三角形,AB=AC,过△ABC的一个顶点的一条直线把△ABC分成的两个小三角形也是等腰三角形,则△ABC各内角度数可能是多少?
如图,已知△ABC是等腰三角形,AB=AC,过△ABC的一个顶点的一条直线把△ABC分成的两个小三角形也是等腰三角形,则△ABC各内角度数可能是多少? 分析 本题要利用三角形内角和定理求解.由于本题中经过等腰三角形顶点的直线没有明确是经过顶角的顶点还是底角的顶点,因此本题要分情况讨论.
解答 解:设该等腰三角形的底角是x;
①如图1,
当过顶角的顶点的直线把它分成了两个等腰三角形,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
∴x+x+x+x=180,
解得x=45,
则顶角是90°;
②如图2,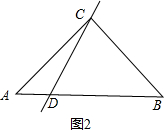
AC=BC=BD,AD=CD,
设∠B=x°,
∵AC=BC,
∴∠A=∠B=x°,
∵AD=CD,
∴∠ACD=∠A=x°,
∴∠BDC=∠A+∠ACD=2x°,
∵BC=BD,
∴∠BCD=∠BDC=2x°,
∴∠ACB=3x°,
∴x+x+3x=180,x=36°,则顶角是108°.
③如图3,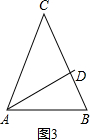
当过底角的角平分线把它分成了两个等腰三角形,则有AC=BC,AB=AD=CD,
设∠C=x°,
∵AD=CD,
∴∠CAD=∠C=x°,
∴∠ADB=∠CAD+∠C=2x°,
∵AD=AB,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠CAB=∠B=2x°,
∵∠CAB+∠B+∠C=180°,
∴x+2x+2x=180,
x=36°,
则顶角是36°.
④如图4,
当∠A=x°,∠ABC=∠ACB=3x°时,也符合,
AD=BD,BC=DC,
∠A=∠ABD=x,∠DBC=∠BDC=2x,
则x+3x+3x=180°,
x=$\frac{180°}{7}$,
因此等腰三角形顶角的度数为36°或90°或108°或$\frac{180°}{7}$.
点评 本题考查了等腰三角形的性质及其判定.作此题的时候,首先大致画出符合条件的图形,然后根据等腰三角形的性质、三角形的内角和定理及其推论找到角之间的关系,列方程求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>3 | B. | a=3 | C. | a≤3 | D. | a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$÷$\frac{1}{\sqrt{3}}$=$\sqrt{\frac{12}{3}}$=$\sqrt{4}$=2 | B. | $\sqrt{2\frac{1}{2}}$÷$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | ||
| C. | $\sqrt{0.2}$÷$\sqrt{0.6}$=$\sqrt{\frac{0.2}{0.6}}$=$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{-16}}{\sqrt{-2}}$=$\sqrt{\frac{16}{2}}$=$\sqrt{8}$=2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com