
【题目】已知抛物线![]()
![]() 若该抛物线经过点
若该抛物线经过点![]() ,试求
,试求![]() 的值及抛物线的顶点坐标.
的值及抛物线的顶点坐标.
![]() 求此抛物线的顶点坐标(用含
求此抛物线的顶点坐标(用含![]() 的代数式表示) ,并证明:不论
的代数式表示) ,并证明:不论![]() 为何值,该抛物线的顶点都在同一条直线
为何值,该抛物线的顶点都在同一条直线![]() 上.
上.
![]() 直线
直线![]() 截抛物线所得的线段长是否为定值?若是,请求出这个定值;若不是,请说明理由.
截抛物线所得的线段长是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]() ,当
,当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]() ;(2)顶点坐标为
;(2)顶点坐标为![]() ;证明见解析;(3)是,
;证明见解析;(3)是,![]()
【解析】
(1)将点P的坐标代入抛物线解析式中可求出m的值,再利用二次函数的性质可求出抛物线的顶点坐标;
(2)利用配方法找出抛物线的顶点坐标,由其纵坐标减横坐标为定值,可得出不论m为何值,该抛物线的顶点坐标都在同一条直线l上;
(3)将直线l的解析式代入抛物线解析式中可得出关于x的一元二次方程,解之可得出交点的横坐标,利用一次函数图象上点的坐标特征可得出交点的坐标,再利用两点间的距离公式可求出直线l截抛物线所得的线段长.
解:![]() 将
将![]() 代入
代入![]()
得![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]()
当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]()
![]() 方法1:设顶点坐标为
方法1:设顶点坐标为![]()
则![]()
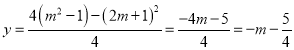
![]() 顶点坐标为
顶点坐标为![]()
方法2:
∵![]()
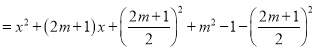
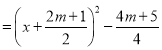
![]() 顶点坐标为
顶点坐标为![]()
证明:∵![]()
![]() 不论
不论![]() 为何值,该抛物线的顶点都在同一条直线
为何值,该抛物线的顶点都在同一条直线![]() 上
上
![]() 是
是
将![]() 代入
代入![]() 得
得
![]()
![]() 与抛物线的交点坐标分别为
与抛物线的交点坐标分别为
![]()
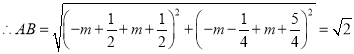


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
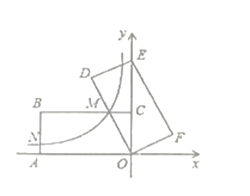
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》内容主要讲数学的用途,浅显易懂,其中有许多有趣的数学题,如“河边洗碗”.原文:今有妇人河上荡桮.津吏问曰:“桮何以多?“妇人曰:“家有客.”津吏曰:“客几何?”妇人日:“二人共饭,三人共羹,四人共肉,凡用桮六十五.不知客几何?“译文:有一名妇女在河边洗刷一大摞碗.一个津吏问她:“怎么刷这么多碗呢?“她回答:“家里来客人了.“津吏又问:“家里来了多少客人?”妇女答道:“2个人给一碗饭,3个人给一碗汤,4个人给一碗肉,一共要用65只碗,来了多少客人?”答:共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
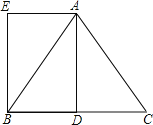
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了![]() 4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
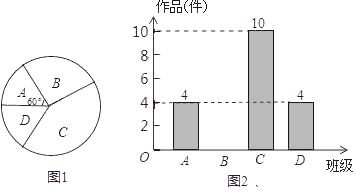
(1)王老师采取的调查方式是 (填“普查”或“抽样调査”),王老师所调查的4个班共征集到作品 件,并补全条形统计图;
(2)在扇形统计图中,表示![]() 班的扇形周心角的度数为 ;
班的扇形周心角的度数为 ;
(3)如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
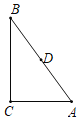
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图①,若点![]() 分别为
分别为![]() 上的点,且
上的点,且![]() ,试探究
,试探究![]() 和
和![]() 的数量关系;并说明四边形
的数量关系;并说明四边形![]() 的面积是定值吗?若是,请求出;若不是,请说明理由.
的面积是定值吗?若是,请求出;若不是,请说明理由.
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
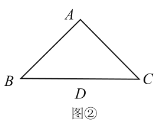
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com