
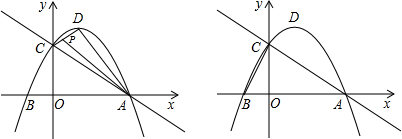
分析 (1)先根据直线y=-$\frac{2}{3}$x+2分别交y轴、x轴于C、A两点,可求C、A两点的坐标,再根据待定系数法可求抛物线的解析式及顶点D的坐标;
(2)根据相似三角形的性质得到P($\frac{1}{3}$,$\frac{20}{9}$),再根据待定系数法可求直线AP的解析式;
(3)分两种情况:①过点A作AQ1⊥AC交CR1与点Q1,过点Q1作Q1K1⊥x轴于点K1,②如图2,过点A作AQ2⊥AC交CR2与点Q2,过点Q2作Q2K2⊥x轴于点K2,进行讨论即可得到m的值.
解答 解:(1)∵直线y=-$\frac{2}{3}$x+2分别交y轴、x轴于C、A两点,
∴x=0时,y=2,C点坐标为(0,2),
y=0时,x=3,A点坐标为(3,0),
∵抛物线y=ax2+bx+c(a≠0)经过点C和点A,且过点B(-1,0),
∴$\left\{\begin{array}{l}{c=2}\\{9a+3b+c=0}\\{a-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{4}{3}}\\{c=2}\end{array}\right.$.
∴抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2,顶点坐标为D(1,$\frac{8}{3}$);
(2)过点D作DS∥y轴,过点C作CS∥x轴交DS于点S,过点P作PK∥y轴交CS于点K,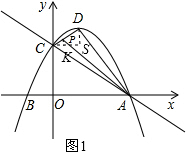 ∴△CKP∽△CSD,
∴△CKP∽△CSD,
∴$\frac{PK}{DS}$=$\frac{CP}{CD}$=$\frac{CK}{CS}$,
∵S△ACP:S△ADP=1:2,
∴CP:PD=1:2,
∴$\frac{PK}{DS}$=$\frac{CP}{CD}$=$\frac{CK}{CS}$=$\frac{1}{3}$,
∵DS=$\frac{2}{3}$,CS=1,
∴PK=$\frac{2}{9}$,CK=$\frac{1}{3}$,
∴P($\frac{1}{3}$,$\frac{20}{9}$),
设AP所在的直线为:y=k2x+b2(k2≠0),则
$\left\{\begin{array}{l}{3{k}_{2}+{b}_{2}=0}\\{\frac{1}{3}{k}_{2}+{b}_{2}=\frac{20}{9}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=-\frac{5}{6}}\\{{b}_{2}=\frac{5}{2}}\end{array}\right.$.
∴y=-$\frac{5}{6}$x+$\frac{5}{2}$.
(3)①如图2,过点A作AQ1⊥AC交CR1与点Q1,过点Q1作Q1K1⊥x轴于点K1,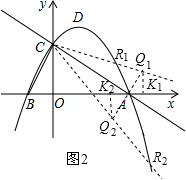 ∵OC=2,OB=1,
∵OC=2,OB=1,
∴tan∠BCO=$\frac{1}{2}$,
∵∠ACR=∠BCO,
∴在Rt△CAQ1中,tan∠ACR=$\frac{1}{2}$,AC=$\sqrt{13}$,
∴Q1A=$\frac{\sqrt{13}}{2}$,
∵△AOC∽△AK1Q1,
∴AK1:Q1K1:AQ1=2:3:$\sqrt{13}$,
∴Q1(4,$\frac{3}{2}$),
∴CQ1所在的直线:y=-$\frac{1}{8}$x+2,
联立$\left\{\begin{array}{l}{y=-\frac{1}{8}x+2}\\{y=-\frac{2}{3}{x}^{2}+\frac{4}{3}x+2}\end{array}\right.$,
解得:x1=0(舍去),x2=$\frac{35}{16}$,
∴m=$\frac{35}{16}$.
②如图2,过点A作AQ2⊥AC交CR2与点Q2,过点Q2作Q2K2⊥x轴于点K2,
由①知道:△AK1Q1≌△AK2Q2,
∴Q2(2,-$\frac{3}{2}$),
∴CQ2所在的直线:y=-$\frac{7}{4}$x+2.
联立$\left\{\begin{array}{l}{y=-\frac{7}{4}x+2}\\{y=-\frac{2}{3}{x}^{2}+\frac{4}{3}x+2}\end{array}\right.$,
解得:x1=0(舍去),x2=$\frac{37}{8}$.
∴m=$\frac{37}{8}$.
点评 考查了二次函数综合题,涉及二次函数的图象与性质、一次函数的图象与性质、待定系数法、相似三角形的性质等重要知识点,涉及考点众多,有一定的难度.第(3)问注意分类思想的应用.


科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
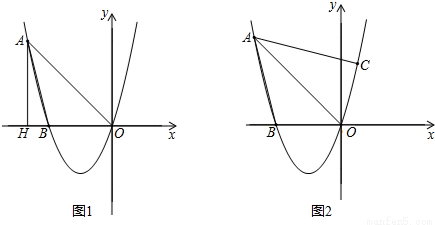
已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
盐城市2015年初中毕业生人数达10.1万.数据10.1万用科学记数法表示为( )
A. 1.01×10 B. 10.1×104 C. 1.01×105 D. 0.101×106
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
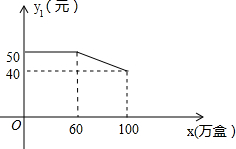 有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=$\left\{\begin{array}{l}{40(0≤x≤60)}\\{\frac{3}{4}x+5(60<x≤100)}\end{array}\right.$
有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=$\left\{\begin{array}{l}{40(0≤x≤60)}\\{\frac{3}{4}x+5(60<x≤100)}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2b | B. | -2c | C. | 2a-2c | D. | 2a-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若有理数a、b、c在数轴上的位置如图所示,其中O是原点,|b|=|c|.
若有理数a、b、c在数轴上的位置如图所示,其中O是原点,|b|=|c|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com