
 若有理数a、b、c在数轴上的位置如图所示,其中O是原点,|b|=|c|.
若有理数a、b、c在数轴上的位置如图所示,其中O是原点,|b|=|c|.分析 (1)根据数轴是表示数的一条直线,可把数在数轴上表示出来;根据数轴上的点表示的数右边的总比左边的大,可得答案;
(2)根据互为相反数的和为零,可得答案;
(3)根据同号两数相加,取相同的符号,绝对值相加;异号两数相加,取绝对值较大加数的符号,用较大的绝对值减较小的绝对值,可得答案.
解答 解:(1)如图: ,
,
由数轴上的点表示的数右边的总比左边的大,得
a<b<-b<-a;
(2)∵b<0<c,|b|=|c|,
即b=-c,b+c=0;
(3)∵a<b<0,
∴a+b<0;
∵a<b<0,
∴|a|>|b|.
∵|b|=|c|,|a|>|c|,
∴a+c<0.
点评 本题考查了有理数大小比较,数轴上的点表示的数右边的总比左边的大,熟记有理数的加法法则并根据法则计算是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
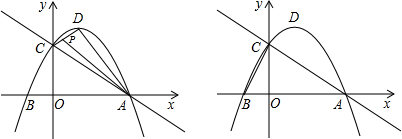
 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{1}{2x}$ | C. | y=x-1 | D. | y=$\frac{x}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 存入(+)/支出(-) | 余额 |
| 20150630 | +3200 | 13500 |
| 20150715 | -7450 | |
| 20150820 | +1500 |
| A. | 19450元 | B. | 8550元 | C. | 7650元 | D. | 7550元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
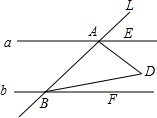 如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )
如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )| A. | 45° | B. | 50° | C. | 60° | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com