
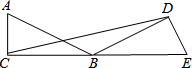
 如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时旋转角的度数是150°.
如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时旋转角的度数是150°. 科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:单选题
如图,点O在直线AB上,且OC⊥OD,若∠COA=35°,则∠DOB的大小为( )
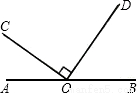
A. 35° B. 45° C. 55° D. 65°
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
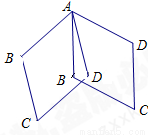
如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向
旋转,得菱形AB′C′D′1,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
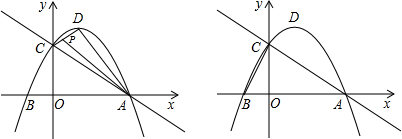
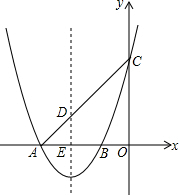 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
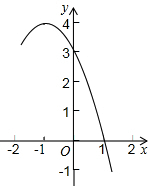 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
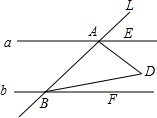 如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )
如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )| A. | 45° | B. | 50° | C. | 60° | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com