
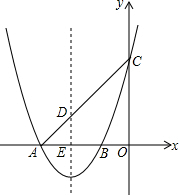
 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,分析 (1)根据二次函数y=ax2+bx+c的对称轴为x=-$\frac{b}{2a}$,求得抛物线的对称轴,因为函数与X轴的交点是y=0,列方程即可求得;
(2)分别以AC,AB为对角线各可求得一点,再以AC,AB为边求得一点.
解答 解:(1)①对称轴x=-$\frac{4}{2}$=-2;
②当y=0时,有x2+4x+3=0,
解得x1=-1,x2=-3,
故点A的坐标为(-3,0).
(2)如图所示,满足条件的点P有3个,分别为(-2,3),(2,3),(-4,-3).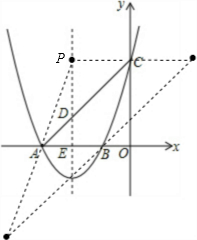
点评 此题考查了二次函数综合题,涉及二次函数与一次函数,四边形的综合知识,解题的关键是要注意数形结合思想的应用.此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.运用上述知识,解决下列问题:
(1)如果(a-2)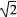 +b+3=0,其中a、b为有理数,那么a=______________;
+b+3=0,其中a、b为有理数,那么a=______________;
(2)如果(2+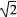 )a-(1-
)a-(1-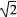 )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
盐城市2015年初中毕业生人数达10.1万.数据10.1万用科学记数法表示为( )
A. 1.01×10 B. 10.1×104 C. 1.01×105 D. 0.101×106
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
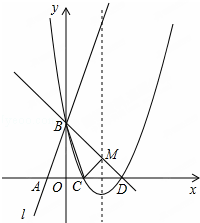 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 大圆外 | B. | 小圆内 | C. | 大圆内,小圆外 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com