
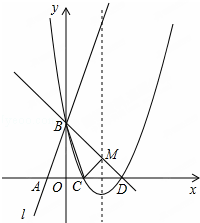
 ��ͼ��ʾ��ֱ��l��y=3x+3��x�ύ�ڵ�A����y�ύ�ڵ�B���ѡ�AOB��y�ᷭ�ۣ���A�䵽��C�������߹���B��C��D��3��0����
��ͼ��ʾ��ֱ��l��y=3x+3��x�ύ�ڵ�A����y�ύ�ڵ�B���ѡ�AOB��y�ᷭ�ۣ���A�䵽��C�������߹���B��C��D��3��0�������� ��1���ɴ���ϵ�������ֱ��BD�������ߵĽ���ʽ��
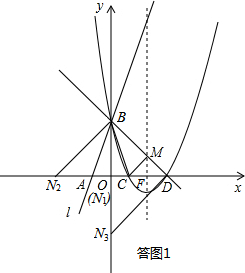
��2������ȷ����MCDΪ����ֱ�������Σ���Ϊ��BND���MCD���ƣ����ԡ�BNDҲ�ǵ���ֱ�������Σ����ͼ1��ʾ�����������ĵ�N��3����
��3�����ͼ2����ͼ3��ʾ������ؼ��������PBD����ı���ʽ��Ȼ�����S��PBD=6����֪�������г�һԪ���η�����⣻
��4��BC���ӳ�����Գ���Ľ���Ϊ��Q�����ô���ϵ�������ֱ��BC�Ľ���ʽ���ٽ�x=2���������Q�������꼴�ɣ�
���  �⣺��1����ֱ��l��y=3x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
�⣺��1����ֱ��l��y=3x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��-1��0����B��0��3����
�߰ѡ�AOB��y�ᷭ�ۣ���A�䵽��C��
��C��1��0����
��ֱ��BD�Ľ���ʽΪ��y=kx+b��
�ߵ�B��0��3����D��3��0����ֱ��BD�ϣ�
��$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$��
���k=-1��b=3��
��ֱ��BD�Ľ���ʽΪ��y=-x+3��
�������ߵĽ���ʽΪ��y=a��x-1����x-3����
�ߵ�B��0��3�����������ϣ�
��3=a����-1������-3����
��ã�a=1��
�������ߵĽ���ʽΪ��y=��x-1����x-3��=x2-4x+3��
��2�������ߵĽ���ʽΪ��y=x2-4x+3=��x-2��2-1��
�������ߵĶԳ���Ϊֱ��x=2����������Ϊ��2��-1����
ֱ��BD��y=-x+3�������ߵĶԳ��ύ�ڵ�M����x=2����y=1��
��M��2��1����
��Գ�����x�ύ��Ϊ��F����CF=FD=MF=1��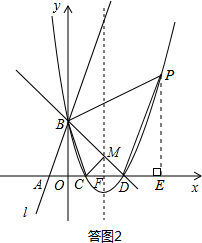
���MCDΪ����ֱ�������Σ�
���Ե�N��B��DΪ��������������MCD���ƣ�
���BNDΪ����ֱ�������Σ�
���ͼ1��ʾ��
��I����BDΪб�ߣ�����֪��ʱֱ�Ƕ���Ϊԭ��O��
��N1��0��0����
��II����BDΪֱ�DZߣ�BΪֱ�Ƕ��㣬���N��x�Ḻ�����ϣ�
��OB=OD=ON2=3��
��N2��-3��0����
��III����BDΪֱ�DZߣ�DΪֱ�Ƕ��㣬���N��y�Ḻ�����ϣ�
��OB=OD=ON3=3��
��N3��0��-3����
�����������ĵ�N����Ϊ����0��0������-3��0����0��-3����
��3��������ڵ�P��ʹS��PBD=6�����P����Ϊ��m��n����
��I������Pλ��ֱ��BD�Ϸ�ʱ�����ͼ2��ʾ��
����P��PE��x���ڵ�E����PE=n��DE=m-3��
S��PBD=S����PEOB-S��BOD-S��PDE=$\frac{1}{2}$��3+n��•m-$\frac{1}{2}$��3��3-$\frac{1}{2}$��m-3��•n=6��
����ã�m+n=7 �٣�
��P��m��n�����������ϣ�
��n=m2-4m+3��
�����ʽ�����ã�m2-3m-4=0��
��ã�m1=4��m2=-1��
��n1=3��n2=8��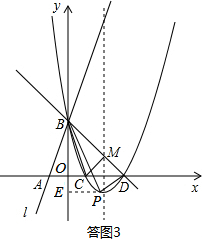 ��P1��4��3����P2��-1��8����
��P1��4��3����P2��-1��8����
��II������Pλ��ֱ��BD�·�ʱ�����ͼ3��ʾ��
����P��PE��y���ڵ�E����PE=m��OE=-n��BE=3-n��
S��PBD=S����PEOD+S��BOD-S��PBE=$\frac{1}{2}$��3+m��•��-n��+$\frac{1}{2}$��3��3-$\frac{1}{2}$��3-n��•m=6��
����ã�m+n=-1 �ڣ�
��P��m��n�����������ϣ�
��n=m2-4m+3��
�����ʽ�����ã�m2-3m+4=0����=-7��0���˷����⣮
�ʴ�ʱ��P�����ڣ�
�������������������ϴ��ڵ�P��ʹS��PBD=6����P������Ϊ��4��3����-1��8����
��4����B��0��3����C��1��0����
��ֱ��BC�Ľ���ʽΪ��y=-3x+3��
�൱x=2ʱ��y=-3��2+3=-3��
���Q��2��-3����
���� �������п�ѹ���⣬�ۺϿ����˶��κ�����ͼ�������ʡ�����ϵ���������������ε��ж������ʡ�ͼ��������㡢��һԪ���η��̵�֪ʶ�㣬���������ν�ϡ��������۵���ѧ˼�룮�ڣ�2����3���ʾ�����з������ۣ�����©�⣬�ڣ�4�������öԳ����жϳ���Q��λ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
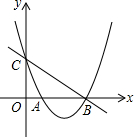 ��֪������C1��y=x2-4x+3��x�ύ��A��B���㣬��y�ύ��C�㣬ƽ��ֱ��BC����PQ����P�ڶԳ����ϣ���Q�ڵ�һ�����������ϣ���CP=QB����Q������꣮
��֪������C1��y=x2-4x+3��x�ύ��A��B���㣬��y�ύ��C�㣬ƽ��ֱ��BC����PQ����P�ڶԳ����ϣ���Q�ڵ�һ�����������ϣ���CP=QB����Q������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�ζ��о��꼶��ѧ�ڵ�һ��ѧ�������ѧ�Ծ��������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��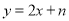 ��
��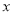 �ᡢ
�ᡢ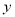 ��ֱ��ڵ�A��B����˫����
��ֱ��ڵ�A��B����˫����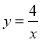 �ڵ�һ�����ڽ��ڵ�C��1��m��.
�ڵ�һ�����ڽ��ڵ�C��1��m��.
��1����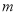 ��
��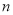 ��ֵ��
��ֵ��
��2����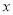 ���ϵĵ�D��
���ϵĵ�D��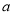 ��0����ƽ����y���ֱ��
��0����ƽ����y���ֱ��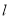 ��
��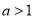 �����ֱ���ֱ��AB��˫����
�����ֱ���ֱ��AB��˫����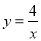 ���ڵ�P��Q����PQ=2QD�����APQ�������
���ڵ�P��Q����PQ=2QD�����APQ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�ζ��о��꼶��ѧ�ڵ�һ��ѧ�������ѧ�Ծ��������棩 ���ͣ������
��ʽ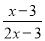 ��ֵΪ0����x��ֵΪ______��
��ֵΪ0����x��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�ζ��о��꼶��ѧ�ڵ�һ��ѧ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
ʹʽ��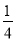 �������xȡֵ��Χ��( )
�������xȡֵ��Χ��( )
A. x����1 B. x�ݣ�1 C. x����1 D. x�ܣ�1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
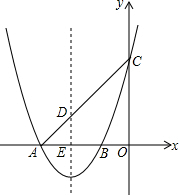 ��ͼ��������y=x2+4x+3��x����A��B���㣬��A��B��ࣩ����y���ڵ�C��
��ͼ��������y=x2+4x+3��x����A��B���㣬��A��B��ࣩ����y���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
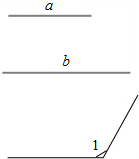 ��֪�߶�a��b�͡�1�������ó߹�����ABC��ʹ��AB=a��AC=b����A=��1��
��֪�߶�a��b�͡�1�������ó߹�����ABC��ʹ��AB=a��AC=b����A=��1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com