
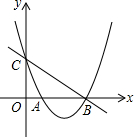
 已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.
已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标. 分析 根据函数解析式可以求得点A、B、C三点的坐标及对称轴的值,从而可得点Q的坐标,由点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,可以求得点Q的坐标,从而可以解答本题.
解答 解:∵y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,
∴y=0时,x=1或x=3;x=0时,y=3;对称轴为:x=$-\frac{-4}{2×1}=2$.
∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3).
∵点P在对称轴上,点Q在第一象限的抛物线上,
∴设点P的坐标为(2,y),点Q的坐标为(x,x2-4x+3).
∵CP=QB,
∴$\sqrt{(2-0)^{2}+(y-3)^{2}}$=$\sqrt{(x-3)^{2}+({x}^{2}-4x+3-0)^{2}}$①.
∵平移直线BC,至PQ,
∴BC∥PQ.
∴$\frac{3-0}{0-3}=\frac{{x}^{2}-4x+3-y}{x-2}$②.
由①②解得,x=2+$\sqrt{3}$或x=2-$\sqrt{3}$或x=5.
∴当x=2+$\sqrt{3}$时,x2-4x+3=2;当x=2-$\sqrt{3}$时,x2-4x+3=2;当x=5时,x2-4x+3=8.
即点Q的坐标为(2+$\sqrt{3}$,2)或(2-$\sqrt{3}$,2)或(5,8).
点评 本题考查坐标与图象的性质,解题的关键是可以求出各点的坐标,根据条件可以列出相应的方程,会解方程组.


科目:初中数学 来源: 题型:解答题
 如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
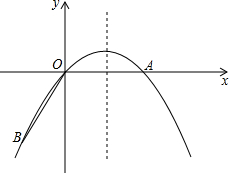
 如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:
如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,登山爱好者在山脚A处测得山顶B处的仰角∠BAC为30°,在坡比为5:12的山坡AD上走1300米到达D处.已知BD的坡比为1:1,则山的高BC为( )米.
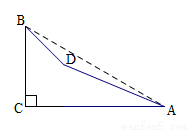
A. 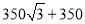 B.
B. 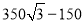 C. 1000 D.
C. 1000 D. 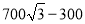
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
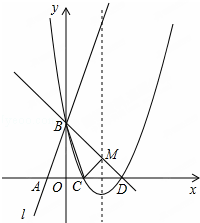 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com