
 如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:
如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:分析 (1)设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值;
(2)设这次跳投时,球出手处离地面hm,因为(1)中求得y=-0.2x2+3.5,当x=-2,5时,即可求得结论.
解答 解:(1)∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得 3.05=a×1.52+3.5,
∴a=-$\frac{1}{5}$,
∴y=-$\frac{1}{5}$x2+3.5.
(2)设这次跳投时,球出手处离地面hm,
因为(1)中求得y=-0.2x2+3.5,
∴当x=-2.5时,
h=-0.2×(-2.5)2+3.5=2.25m.
∴这次跳投时,球出手处离地面2.25m.
点评 本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,体现了数学建模的数学思想,难度不大,能够结合题意利用二次函数不同的表达形式求得解析式是解答本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
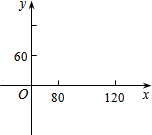 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
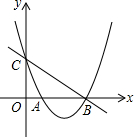 已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.
已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:填空题
写出一个二次项系数为1,且一个根是3的一元二次方程__________.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
使式子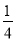 有意义的x取值范围是( )
有意义的x取值范围是( )
A. x>-1 B. x≥-1 C. x<-1 D. x≤-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com