
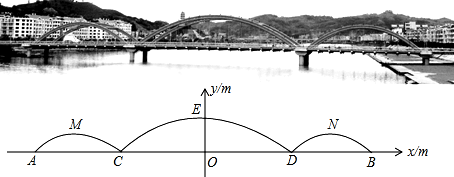
分析 (1)将x=0代入抛物线的解析式就可以直接求出结论.
(2)当y=0时代入抛物线的解析式,求出其交点坐标就可以求出CD的长度,从而就可以BD、CD的值而得出结论.
(3)由(2)的结论可以求出点B、点D的坐标,作NF⊥x轴于点F,连结DE、BN,△NFB∽△EOD就可以求出NF的值而得出N的坐标,再由待定系数法就可以求出结论.
解答 解:(1)∵y=-$\frac{1}{36}$x2+16,
∴当x=0时,y=16,
∴钢梁最高点离桥面的高度OE的长16m;
(2)∵y=-$\frac{1}{36}$x2+16,
∴当y=0时,0=-$\frac{1}{36}$x2+16,
∴x=±24,
∴C(-24,0),D(24,0),
∴DC=48,
∵BD=$\frac{1}{2}$CD,
∴BD=24,
∵左右两条抛物线关于y轴对称,
∴AC=BD=24,
∴AB=48+24+24=96m;
(3)如图,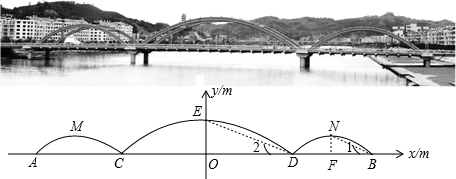
作NF⊥x轴于点F,连结DE、BN
∴∠NFB=∠EOD=90°,DF=BF=10,
∵DE∥BN,
∴∠2=∠1,
∴△NFB∽△EOD,
∴$\frac{BF}{OD}$=$\frac{NF}{OE}$,
∴$\frac{12}{24}$=$\frac{NF}{16}$,
∴NF=8.
∴N(36,8).
设抛物线的解析式为y=a(x-36)2+8,由题意,得
0=a(24-36)2+8,
解得:a=-$\frac{1}{18}$,
∴y=-$\frac{1}{18}$(x-36)2+8.
点评 本题考查了二次函数的运用,轴对称的运用,平行线的性质的运用,相似三角形的判定及性质的运用,抛物线的顶点式的运用,解答时求出抛物线与x轴的交点坐标是关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
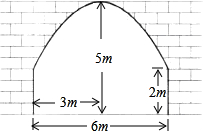 某隧道横断而由抛物线与矩形的三边组成,尺寸如图所示.
某隧道横断而由抛物线与矩形的三边组成,尺寸如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
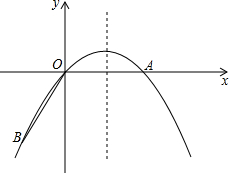 如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:
如图,一位篮球运动员在距离篮圈中心水平距离4m处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落人篮框内,已知篮圈中心距离地面高度为3.05m,试解答下列问题:查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
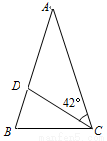
在△ABC中,AB=AC,CD=CB,若∠ACD=42°,则∠BAC=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com