
分析 (1)先化简再计算加减法;
(2)直接运用乘法的分配律计算;
(4)将除法变为乘法再运用乘法的分配律计算;
(3)(5)将除法变为乘法再约分计算即可求解;
(6)(7)(8)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的.
解答 解:(1)-3+5.3-(-7)-5.3
=-3+5.3+7-5.3
=4+0
=4;
(2)$-9\frac{17}{18}×9$
=(-10+$\frac{1}{18}$)×9
=-10×9+$\frac{1}{18}$×9
=-90+$\frac{1}{2}$
=-89$\frac{1}{2}$;
(3)$({-2})×\frac{3}{2}÷(-\frac{3}{4})×4$
=2×$\frac{3}{2}$×$\frac{4}{3}$×4
=16;
(4)$({\frac{5}{12}-\frac{7}{9}-\frac{2}{3}})÷\frac{1}{36}$
=($\frac{5}{12}$-$\frac{7}{9}$-$\frac{2}{3}$)×36
=$\frac{5}{12}$×36-$\frac{7}{9}$×36-$\frac{2}{3}$×36
=15-28-24
=-37;
(5)$({-\frac{3}{4}})×({-1\frac{1}{2}})÷({-2\frac{1}{4}})$
=-$\frac{3}{4}$×$\frac{3}{2}$×$\frac{4}{9}$
=-$\frac{1}{2}$;
(6)(-1)100×5+(-2)4÷4
=1×5+16÷4
=5+4
=9;
(7)-32×1.22÷0.32+(-$\frac{1}{3}$)2×(-3)3÷(-1)2015
=-9×1.44÷0.09+$\frac{1}{9}$×(-27)÷(-1)
=-144+3
=-141;
(8)0.25×(-2)3-[4÷(-$\frac{2}{3}$)2+1]+(-1)2007
=0.25×(-8)-[4÷$\frac{4}{9}$+1]+(-1)
=-2-[9+1]-1
=-2-10-1
=-13.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:填空题
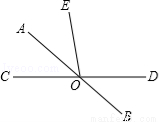
如图,直线AB、CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE= .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com