
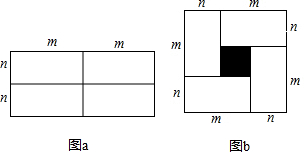
分析 (1)根据图形即可得出图b中小正方形的边长为m-n;
(2)直接利用正方形的面积公式得到图中阴影部分的面积为(m-n)2;也可以用大正方形的面积减去4个长方形的面积得到图中阴影部分的面积为
(m+n)2-4mn;
(3)根据图中阴影部分的面积是定值得到等量关系式;
(4)利用(3)中的公式得到(a-b)2=(a+b)2-4ab.
解答 解:(1)图b中小正方形的边长为m-n.
故答案为m-n;
(2)方法①:(m-n)(m-n)=(m-n)2;
方法②:(m+n)2-4mn;
(3)因为图中阴影部分的面积不变,所以(m-n)2=(m+n)2-4mn;
(4)由(3)得:(a-b)2=(a+b)2-4ab,
∵a+b=7,ab=5,
∴(a-b)2=72-4×5
=49-20
=29.
点评 本题考查了完全平方公式的几何背景,列代数式,可以根据题中的已知数量利用代数式表示其他相关的量.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
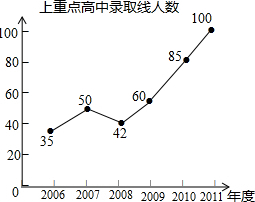 某校近6年来中考上市重点高中录取的情况如图所示:
某校近6年来中考上市重点高中录取的情况如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com