
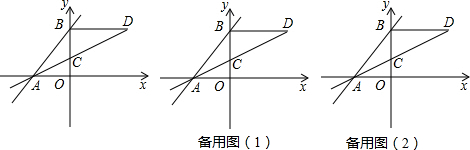
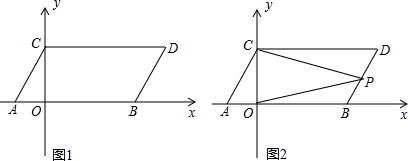
���� ��1������C��CE��AB������ΪE�������A��B��������꣬Ȼ�������AB�ij������ݽ�ƽ���ߵ����ʿ�֪��CE=OC��Ȼ����S��ABO=S��ABC+S��AOC�����OC�ij���Ȼ�����ô���ϵ���������AC�Ľ���ʽ��
��2����ͼ2��ʾ������P��PE��OB������ΪE����PE��OA��֪$\frac{PE}{AO}=\frac{PB}{AB}$���Ӷ��õ�PE=6-$\frac{6}{5}t$��Ȼ�����������ε������ʽ��⼴�ɣ���ͼ3��ʾ������Pλ��BD��ʱ��PB=2t-10��Ȼ�����������ε������ʽ��⼴�ɣ�
��3������CE����OP��ԲC���У������tan��ECO=$\frac{4}{3}$���Ӷ����ֱ��OP�Ľ���ʽΪy=$-\frac{4}{3}x$��Ȼ��ɽ�õ�P������Ϊ��-3��4������F������Ϊ��$-\frac{18}{11}$��$\frac{24}{11}$�����������ľ��빫ʽ���CF�ij������������ݹ��ɶ������EF�ij���������������Ǻ����Ķ��弴����ô𰸣�
��� �⣺��1����ͼ1��ʾ������C��CE��AB������ΪE��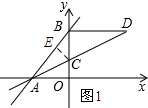
��y=0�ã�$\frac{4}{3}x+8$=0����ã�x=-6��
���A��������-6��0����
��x=0�ã�y=8��
���B��������0��8����
��Rt��ABO��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}=10$��
��ACƽ�֡�BAO��OC��AO��CE��AB��
��CE=OC��
��S��ABO=S��ABC+S��AOC��
��$\frac{1}{2}AO•OB=\frac{1}{2}AB•CE+\frac{1}{2}AO•OC$��
��$\frac{1}{2}��6��8=\frac{1}{2}��10��EC+\frac{1}{2}��6��OC$��
��24=5EC+3OC��
��OC=3��
���C��������0��3����
��ֱ��AC�Ľ���ʽΪy=kx+b������A�͵�C���������ã�$\left\{\begin{array}{l}{-6k+b=0}\\{b=3}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=$\frac{1}{2}x+3$��
��2����ͼ2��ʾ������P��PE��OB������ΪE��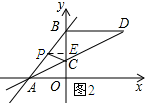
��AO��OB��PE��OB��
��PE��OA��
��$\frac{PE}{AO}=\frac{PB}{AB}$����$\frac{PE}{6}=\frac{10-2t}{10}$��
��PE=6-$\frac{6}{5}t$��
���BCP�����=$\frac{1}{2}BC•PE$=$\frac{1}{2}����8-3������6-\frac{6}{5}t��$=15-3t��0��t��5����
��ͼ3��ʾ������Pλ��BD��ʱ����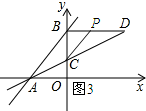
��y=8����y=$\frac{1}{2}x+3$�ã�$\frac{1}{2}x+3=8$��
��ã�x=10��
PB=2t-10��
���PBC�����=$\frac{1}{2}BC•BP$=$\frac{1}{2}��5����2t-10��$=5t-25��5��t��10����
����������s��t�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{15-3t��0��t��5��}\\{5t-25��5��t��10��}\end{array}\right.$��
��3����ͼ4��ʾ������CE��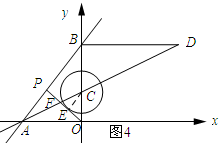
��OP��ԲC���У��е�ΪC��
��CE��OP��
��cos��ECO=$\frac{3}{5}$��
��tan��ECO=$\frac{4}{3}$��
��ֱ��OP�Ľ���ʽΪy=$-\frac{4}{3}x$��
��y=$-\frac{4}{3}x$��y=$\frac{4}{3}x+8$������$\left\{\begin{array}{l}{y=-\frac{4}{3}x}\\{y=\frac{4}{3}x+8}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=-3}\\{y=4}\end{array}\right.$��
���P��������-3��4����
�������ľ��빫ʽ�ã�AP=$\sqrt{[-6-��-3��]^{2}+��4-0��^{2}}$=5��
��2t=5��
��t=2.5��
��y=$\frac{1}{2}x+3$��y=$-\frac{4}{3}x$�����ã�$\left\{\begin{array}{l}{y=\frac{1}{2}x+3}\\{y=-\frac{4}{3}x}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=-\frac{18}{11}}\\{y=\frac{24}{11}}\end{array}\right.$��
���F��������$-\frac{18}{11}$��$\frac{24}{11}$����
�������ľ��빫ʽ�ã�CF=$\sqrt{��\frac{18}{11}��^{2}+��3-\frac{24}{11}��^{2}}$=$\frac{9\sqrt{5}}{11}$��
��Rt��ECF��EF=$\sqrt{F{C}^{2}-E{C}^{2}}$=$\frac{18}{55}$��
��tan��CFE=$\frac{CE}{EF}$=$\frac{11}{2}$��
��ͼ5��ʾ������CE��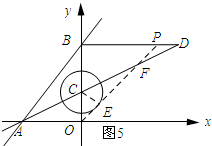
��OP��ԲC�����ߣ�
��CE��OP��
��OC=3��OE=1.8��
�ɹ��ɶ����ã�OE=2.4��
��tan$��OCE=\frac{4}{3}$��
��ֱ��OP�Ľ���ʽΪy=$\frac{4}{3}x$��
��y=8�ã�$\frac{4}{3}x=8$����ã�x=6��
���P��������6��8����
��2t=10+6��
���t=8��
��y=$\frac{1}{2}x+3$��y=$\frac{4}{3}x$������$\left\{\begin{array}{l}{y=\frac{1}{2}x+3}\\{y=\frac{4}{3}x}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=\frac{18}{5}}\\{y=\frac{24}{5}}\end{array}\right.$
���F��������$\frac{18}{5}$��$\frac{24}{5}$����
�������ľ��빫ʽ�ã�CF2=$��\frac{18}{5}��^{2}+��\frac{24}{5}-3��^{2}$=$\frac{81}{5}$��
��Rt��CEF��EF=$\sqrt{C{F}^{2}-C{E}^{2}}$=$\sqrt{\frac{81}{5}-��\frac{9}{5}��^{2}}$=$\frac{18}{5}$��
tan��CFE=$\frac{EC}{EF}$=$\frac{1}{2}$��
���� ������Ҫ�������һ�κ������ۺ�Ӧ�ã������ε������ʽ�����ߵ����ʡ����ɶ����������ľ��빫ʽ�����ֱ��OP�Ľ���ʽ�Լ���P�͵�F�������ǽ���Ĺؼ���


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1cm | B�� | 2cm | C�� | 3cm | D�� | 4cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AD��BE��CF�ǡ�O��ֱ�����ҡ�AOF=��BOC=��DOE����AB��CD��EF�����Ϊʲô��
��ͼ��AD��BE��CF�ǡ�O��ֱ�����ҡ�AOF=��BOC=��DOE����AB��CD��EF�����Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com