Question

10．如图1，在平面直角坐标系中，点A，B的坐标分别为A（m，0），B（n，0）且m、n满足|m+2|+$\sqrt{5-n}$=0，现同时将点A，B分别向上平移3个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）$\frac{∠DCP+∠BOP}{∠CPO}$的值是否发生变化，并说明理由．．
（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S_△PCD=S_△PBD；S_△POB：S_△POC=5：6，若存在这样一点，求出点P的坐标，若不存在，试说明理由． 

Answer 1

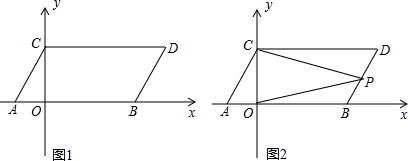
分析 （1）根据非负数的性质得到m=-2，n=5，求得A（-2，0），B（5，0），根据平移的性质得到点C（0，3），D（7，3）；即可得到结果；
（2）过点P作PE∥CD，根据两直线平行，内错角相等可得∠DCP=∠CPE，根据平行公理可得PE∥AB，再根据两直线平行，内错角相等可得∠BOP=∠OPE，然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO，再求出比值即可；
（3）如图3，过P作PM⊥OB于M，并反向延长交CD于N，设P（m，n），根据S_△POB：S_△POC=5：6，于是得到$\frac{1}{2}$×5•n=$\frac{1}{2}×3•m$，求得m=$\frac{5}{3}$n，①由于S_△PCD=S_△PBD，于是得到$\frac{1}{2}$×7•（3-n）=$\frac{1}{2}$（5-m+7-m）×3-$\frac{1}{2}$（5-m）n-$\frac{1}{2}$（7-m）（3-n），②解方程组即可得到结论．

解答 解：（1）∵|m+2|+$\sqrt{5-n}$=0，
∴m=-2，n=5，
∴A（-2，0），B（5，0），
∵点A，B分别向上平移3个单位，再向右平移2个单位，
∴点C（0，3），D（7，3）；
∵OB=5，
∴S_{四边形OBDC}=$\frac{1}{2}$（5+7）×3=18；

（2）$\frac{∠DCP+∠BOP}{∠CPO}$=1，比值不变．
理由如下：由平移的性质可得AB∥CD，
如图，过点P作PE∥AB，则PE∥CD，
∴∠DCP=∠CPE，∠BOP=∠OPE，
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP，
∴$\frac{∠DCP+∠BOP}{∠CPO}$=1，比值不变；

（3）存在，
如图3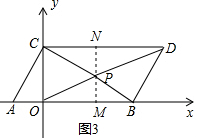，过P作PM⊥OB于M，并反向延长交CD于N，
∵CD∥OB，
∴PN⊥CD，
设P（m，n），
∵S_△POB：S_△POC=5：6，
∴$\frac{1}{2}$×5•n=$\frac{1}{2}×3•m$，
∴m=$\frac{5}{3}$n，①
∵S_△PCD=S_△PBD，
∴$\frac{1}{2}$×7•（3-n）=$\frac{1}{2}$（5-m+7-m）×3-$\frac{1}{2}$（5-m）n-$\frac{1}{2}$（7-m）（3-n），
化简得-3m+9n=6②，
把①代入②，解得：m=4，n=2，
∴P（4，2）．
∴存在这样一点P，使S_△PCD=S_△PBD；S_△POB：S_△POC=5：6．

点评 本题考查了坐标与图形性质，平行线的性质，三角形的面积，坐标与图形变化-平移，熟记各性质是解题的关键．