
 如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.弦AB、CD、EF相等吗?为什么?
如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.弦AB、CD、EF相等吗?为什么?  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 小明在八年级上学期的数学成绩如表所示:
小明在八年级上学期的数学成绩如表所示:| 平时 | 期中 | 期末 | ||||
| 测验1 | 测验2 | 测验3 | 课题学习 | |||
| 成绩 | 88 | 70 | 98 | 86 | 90 | 87 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
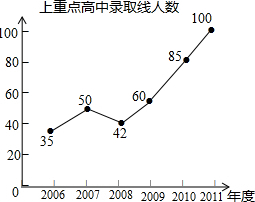 某校近6年来中考上市重点高中录取的情况如图所示:
某校近6年来中考上市重点高中录取的情况如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com