
分析 (1)根据幂的乘方、零指数幂、负整数指数幂可以解答本题;
(2)根据分式的减法和除法可以解答本题.
解答 解:(1)(-2)2+($\sqrt{3}$-1)0-$\sqrt{4}$-($\frac{1}{2}$)-1
=4+1-2-2
=1;
(2)($\frac{{x}^{2}}{x-1}$-$\frac{2x}{1-x}$)÷$\frac{x}{x-1}$
=$\frac{{x}^{2}+2x}{x-1}×\frac{x-1}{x}$
=$\frac{x(x+2)}{x-1}×\frac{x-1}{x}$
=x+2.
点评 本题考查分式的混合运算、实数的运算、零指数幂、负整数指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题:
如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
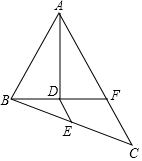 如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.
如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
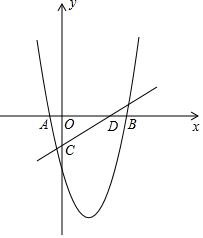 如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.
如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
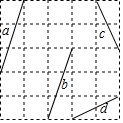 如图,在5×5的正方形网格中,每个小正方形的顶点叫做格点,线段a、b、c、d的端点都在格点上,通过平移其中的两条线段,使得与第三条线段首尾相接组成三角形
如图,在5×5的正方形网格中,每个小正方形的顶点叫做格点,线段a、b、c、d的端点都在格点上,通过平移其中的两条线段,使得与第三条线段首尾相接组成三角形查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com