
|


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
| A、某次地震中,伤亡10万人 |
| B、吐鲁番盆地低于海平面155m |
| C、小明班上有45人 |
| D、小红测得数学书的长度为21.0cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
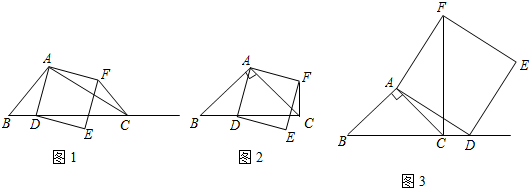
 如图,A,F,C,D四点在同一直线上,AF=CD,AB∥DE,且AB=DE.
如图,A,F,C,D四点在同一直线上,AF=CD,AB∥DE,且AB=DE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 7 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
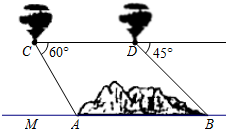 如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据:
如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com