
【题目】用小立方块搭一几何体,它的主视图和俯视图如图所示,这个几何体最少要a个立方块,最多要b个立方块.

(1)求a,b的值
(2)若有理数x,y满足![]() ,
,![]() ,且xy<0,求x+y的值.
,且xy<0,求x+y的值.
【答案】(1)a=10,b=14;(2)4或4
【解析】
(1)由几何体的主视图和俯视图可知,该几何体的主视图第一列3个正方形中每个正方形所在位置最多均可有2个立方块,最少一个正方体所在位置有2个立方块,其余2个所在位置各有1个立方块;主视图第二列1个正方形所在位置只能有2个立方块;主视图第三列每个正方形所在位置最多均可有3个立方块,最少一个正方体所在位置有3个立方块,另外一个所在位置有1个立方块;
(2)将(1)中求得的答案代入条件,根据有理数的乘法运算法则和绝对值的性质判断出x、y的值,然后相加即可得结果.
解:(1)由主视图和俯视图可知:
这样的几何体最少需要(2+1+1)+2+(3+1)=10(个)立方块;
最多需要:2×3+2+3×2=14(个)立方块;
所以a=10,b=14;
(2)由(1)可得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为xy<0,即x、y的符号相反,
当![]() ,则
,则![]() ,此时x+y=1014=4,
,此时x+y=1014=4,
当![]() ,则
,则![]() ,此时x+y=10+14=4,
,此时x+y=10+14=4,
所以x+y的值为4或4.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
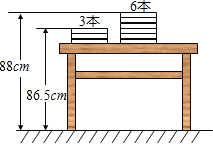
【题目】如图,两摞规格完全相同的课本整齐叠放在讲台上请根据图中所给出的数据信息,回答下列问题:
(1)每本课本的厚度为______cm;
(2)若有一摞上述规格的课本x本,整齐叠放在讲台上,请用含x的代数式表示出这一摞数学课本的顶部距离地面的高度为______cm;
(3)当x=48时,若从中取走10本,求余下的课本的顶部距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
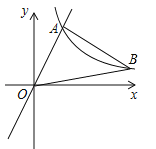
【题目】(2017山东省日照市)如图,在平面直角坐标系中,经过点A的双曲线![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为______.
,∠AOB=∠OBA=45°,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
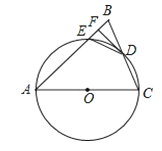
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 都在数轴上,
都在数轴上,![]() 为原点.
为原点.
(1)点![]() 表示的数是 ;
表示的数是 ;
(2)若点![]() 以每秒3个单位长度的速度沿数轴运动,则1秒后点
以每秒3个单位长度的速度沿数轴运动,则1秒后点![]() 表示的数是 ;
表示的数是 ;
(3)若点![]() 都以每秒3个单位长度的速度沿数轴向右运动,而点
都以每秒3个单位长度的速度沿数轴向右运动,而点![]() 不动,
不动,![]() 秒后有一个点是一条线段的中点,求
秒后有一个点是一条线段的中点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D的坐标分别为(-2,2),(一2,1),(3,1),(3,2),线段AD、AB、BC组成的图形记作G,点P沿D-A-B-C移动,设点P移动的距离为a,直线l:y=-x+b过点P,且在点P移动过程中,直线l随点P移动而移动,若直线l过点C,求
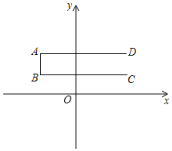
(1)直线l的解析式;
(2)求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.

(1)如果∠BOC=30°,求∠MON的度数;
(2)如果∠AOB=α,∠BOC=30°,其他条件不变,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com