
分析 首先根据点D在⊙C内,点B在⊙C外,求得⊙C的半径是大于3而小于4;再根据勾股定理求得AC=5,最后根据两圆的位置关系得到其数量关系.
解答 解:∵在矩形ABCD中,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵点D在⊙C内,点B在⊙C外,
∴⊙C的半径R的取值范围为:3<R<4,
∴当⊙A和⊙C内切时,圆心距等于两圆半径之差,则r的取值范围是8<r<9;
当⊙A和⊙C外切时,圆心距等于两圆半径之和是5,设⊙C的半径是Rc,即Rc+r=5,
又∵3<Rc<4,
则r的取值范围是1<r<2.
所以半径r的取值范围是8<r<9或1<r<2.
故答案为:8<r<9或1<r<2.
点评 此题综合考查了点和圆的位置关系以及两圆的位置关系与数量关系之间的等价关系.同时注意勾股定理的运用.特别注意两圆相切,可能内切或外切.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
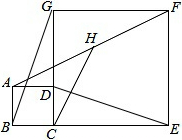 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com