
分析 (1)将方程两边都乘以分母的最小公倍数20,去分母后依次移项、合并同类项、系数化为1可得;
(2)先将方程中得分母化为整数,再按照解方程的基本步骤求解即可.
解答 解:(1)去分母,得:15x=20-4x,
移项,得:15x+4x=20,
合并同类项,得:19x=20,
系数化为1,得:x=$\frac{20}{19}$;
(2)将方程分母化为整数,得:$\frac{10x-30}{3}$-$\frac{10x+10}{5}$=1.2,
去分母,得:5(10x-30)-3(10x+10)=18,
去括号,得:50x-150-30x-30=18,
移项,得:50x-30x=18+150+30,
合并同类项,得:20x=198,
系数化为1,得:x=$\frac{99}{10}$.
点评 本题主要考查解一元一次方程的能力,对于带分母的方程:去分母时,方程两端同乘各分母的最小公倍数,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
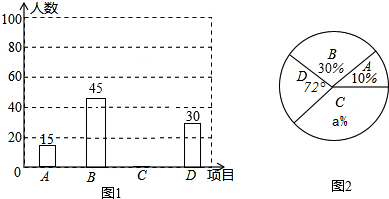
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
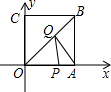 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )| A. | 5 | B. | $\sqrt{10}$ | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
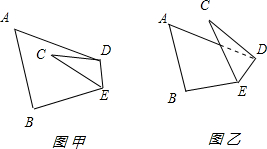
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
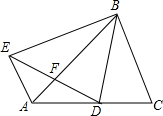 在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.
在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com