
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
分析 首先根据已知将各数化为分子相同,进而比较分母得出各数的大小.
解答 解:∵a=$\sqrt{2}$=$\frac{2}{\sqrt{2}}$=$\frac{4}{\sqrt{2}+\sqrt{2}}$,
b=$\sqrt{7}-\sqrt{3}$=$\frac{(\sqrt{7}-\sqrt{3})(\sqrt{7}+\sqrt{3})}{\sqrt{7}+\sqrt{3}}$=$\frac{4}{\sqrt{7}+\sqrt{3}}$,
c=$\sqrt{6}-\sqrt{2}$=$\frac{(\sqrt{6}-\sqrt{2})(\sqrt{6}+\sqrt{2})}{\sqrt{6}+\sqrt{2}}$=$\frac{4}{\sqrt{6}+\sqrt{2}}$,
$\sqrt{2}+\sqrt{2}$<$\sqrt{6}+\sqrt{2}$<$\sqrt{7}+\sqrt{3}$,
∴b<c<a,
故选:B.
点评 此题主要考查了实数比较大小,正确将各数化为分子相同的数字是解题关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
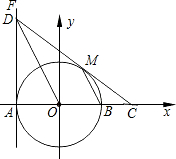 如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com