
分析 先根据题意找出规律,再根据有理数的加减法则进行计算即可.
解答 解:∵$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=$\sqrt{1+1+\frac{1}{4}}$=$\sqrt{\frac{9}{4}}$=1+$\frac{1}{2}$,
$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=$\sqrt{1+\frac{1}{4}+\frac{1}{9}}$=1+$\frac{1}{6}$,…,
∴$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{{(n+1)}^{2}}}$=$\sqrt{\frac{{n}^{2}(n+1)^{2}+{n}^{2}+(n+1)^{2}}{[n(n+1)]^{2}}}$
=$\sqrt{\frac{[n(n+1)]^{2}+2n(n+1)+1}{[n(n+1)]^{2}}}$
=$\sqrt{\frac{({n}^{2}+n+1)^{2}}{{[n(n+1)]}^{2}}}$
=$\frac{{n}^{2}+n+1}{n(n+1)}$
=1+$\frac{1}{n(n+1)}$,
∴原式=(1+$\frac{1}{1×2}$)+(1+$\frac{1}{2×3}$)+(1+$\frac{1}{3×4}$)+…+(1+$\frac{1}{2012×2013}$)
=2012+($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2012×2013}$)
=2012+(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{2012}$-$\frac{1}{2013}$)
=2013-$\frac{1}{2013}$
=2012$\frac{1}{2013}$.
点评 本题考查的是二次根式的加减法,此题属规律性题目,难度较大.


科目:初中数学 来源: 题型:解答题
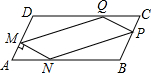 在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.
在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
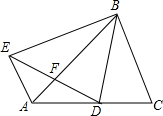 在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.
在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
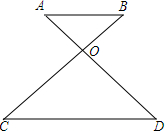 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com