
分析 (1)首先计算幂的乘方,然后利用单项式乘以单项式的方法计算,最后根据a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数)进行计算即可;
(2)首先计算幂的乘方,然后利用单项式乘以单项式的方法计算,最后根据a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数)进行计算即可.
解答 解:(1)原式=a-6•a-3b-6=a-9b-6=$\frac{1}{{a}^{9}{b}^{6}}$;
(2)原式=a-6b2•a-6b4=a-12b6=$\frac{{b}^{6}}{{a}^{12}}$.
点评 此题主要考查了负整数指数幂,关键是掌握计算顺序,掌握a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数).


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
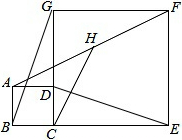 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.
如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
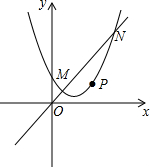 如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com