练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．解方程$\frac{1}{2}${x-$\frac{1}{2}$[x-$\frac{1}{4}$（x-$\frac{2}{3}$）-$\frac{3}{2}$]}=x+$\frac{3}{4}$．

    分析 去括号、去分母、移项、合并同类项、系数化为1，

    解答 解：$\frac{1}{2}${x-$\frac{1}{2}$[x-$\frac{1}{4}$（x-$\frac{2}{3}$）-$\frac{3}{2}$]}=x+$\frac{3}{4}$，
    x-$\frac{1}{2}$[x-$\frac{1}{4}$（x-$\frac{2}{3}$）-$\frac{3}{2}$]=2x+$\frac{3}{2}$，
    -$\frac{1}{2}$[x-$\frac{1}{4}$（x-$\frac{2}{3}$）-$\frac{3}{2}$]=x+$\frac{3}{2}$，
    x-$\frac{1}{4}$（x-$\frac{2}{3}$）-$\frac{3}{2}$=-2x-3，
    x-$\frac{1}{4}$x+$\frac{1}{6}$-$\frac{3}{2}$=-2x-3，
    12x-3x+2-18=-24x-36，
    33x=-20，
    x=-$\frac{20}{33}$．

    点评 考查了解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x=a形式转化．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．如图，已知△ABC，△DCE是两个全等的等腰三角形，底边BC、CE在同一直线上，且AB=$\sqrt{2}$，BC=1，BD与AC交于点P．
    （1）求证：△BED∽△DEC；
    （2）求△DPC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图所示，Rt△ABC中，∠C=90°，AC=4，BC=3，以△ABC的一边为边画等腰三角形，使它的第三个顶点在△ABC的其他边上．请在图①、②、③中分别画出一个符合条件的等腰三角形，且三个图形中的等腰三角形各不相同，且在图中标明所画等腰三角形的腰长．（不要求尺规作图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解下列方程：
    （1）$\frac{3}{4}$x=1-$\frac{1}{5}$x
    （2）$\frac{x-3}{0.3}$-$\frac{x+1}{0.5}$=1.2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．解关于x的方程x+$\frac{ab}{x}$=a+b的根为：x=a或x=b，如①x+$\frac{2}{x}$=3的根为x=1或x=2；②x+$\frac{6}{x}$=5的根为x=2或x=3，求关于x的方程x+$\frac{{n}^{2}+n}{x-3}$=2n+4（n为正整数）的根，你的答案是：n+3或n+4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

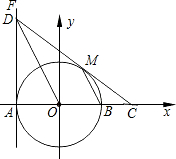    15．如图，在平面直角坐标系xOy中，⊙O交x轴于A，B两点，直线FA⊥x轴于点A，点D在FA上，且DO平行⊙O的弦MB，连DM并延长交x轴于点C．
    （1）判断直线DC与⊙O的位置关系，并证明；
    （2）设点D的坐标为（-6，12），C的坐标为（10，0），试求MC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{201{2}^{2}}+\frac{1}{201{3}^{2}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．?ABCD中，E、F分别是CD、AD边上的点，且AE=CF，AE，CF交于点P，求证：PB平分∠APC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如果一个角的补角是110°，则这个角的余角的度数是（　　）
    A．30°B．20°C．70°D．110°

    查看答案和解析>>

    同步练习册答案