
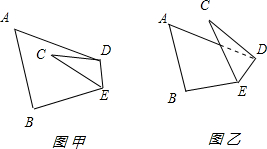
分析 (1)首先根据四边形内角和定理可得:∠ADC+∠BEC+(180°-∠C)+∠A+∠B=360°,整理可得结论;
(2)利用四边形的内角和定理和三角形的内角和定理可得∠BEC+∠CED+∠ADE=180°+∠C,再利用三角形的内角和定理可得∠CED+∠ADE=180°-∠C-∠ADC,再代入整理即可得出结论.
解答 (1)证明:∵∠ADC+∠BEC+(180°-∠C)+∠A+∠B=360°
∴∠ADC+∠BEC=360°-(180°-∠C)-∠A-∠B=180°-∠A-∠B+∠C=2∠C;
(2)解:∠BEC-∠ADC=2∠C.
∵∠BEC+∠CED+∠ADE=360°-(∠A+∠B),∠A+∠B=180°-∠C,
∴∠BEC+∠CED+∠ADE=180°+∠C,
∵∠CED+∠ADE+∠ADC=180°-∠C,
∴∠CED+∠ADE=180°-∠C-∠ADC,
∴∠BEC+(180°-∠C-∠ADC)=180°+∠C,
∴∠BEC-∠ADC=2∠C.
点评 该题主要考查了翻折变换的性质、三角形内角和定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、三角形内角和定理来分析、判断、推理或解答.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 6 | C. | 12 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
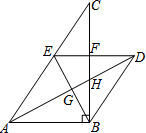 如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.
如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
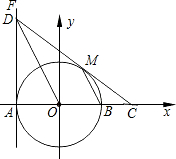 如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com