Question

如图，抛物线y=－x2＋bx＋c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3，

(1)求抛物线所对应的函数解析式；

(2)求△ABD的面积；

(3)将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．

 

 

Answer 1

（1）y=-x2+2x+3；（2）8；（3）点G不在该抛物线上．

【解析】

试题分析：（1）在矩形OCEF中，已知OF、EF的长，先表示出C、E的坐标，然后利用待定系数法确定该函数的解析式．

（2）根据（1）的函数解析式求出A、B、D三点的坐标，以AB为底、D点纵坐标的绝对值为高，可求出△ABD的面积．

（3）首先根据旋转条件求出G点的坐标，然后将点G的坐标代入抛物线的解析式中直接进行判定即可．

（1）∵四边形OCEF为矩形，OF=2，EF=3，

∴点C的坐标为（0，3），点E的坐标为（2，3）．

把x=0，y=3；x=2，y=3分别代入y=-x2+bx+c中，

得，

解得，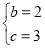

∴抛物线所对应的函数解析式为y=-x2+2x+3；

（2）∵y=-x2+2x+3=-（x-1）2+4，

∴抛物线的顶点坐标为D（1，4），

∴△ABD中AB边的高为4，

令y=0，得-x2+2x+3=0，

解得x1=-1，x2=3，

所以AB=3-（-1）=4，

∴△ABD的面积=×4×4=8；

（3）△AOC绕点C逆时针旋转90°，CO落在CE所在的直线上，由（2）可知OA=1，

∴点A对应点G的坐标为（3，2），

当x=3时，y=-32+2×3+3=0≠2，所以点G不在该抛物线上．

考点：二次函数综合题．