
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)

【答案】2.3.
【解析】
据题意得出tanB =![]() , 即可得出tanA, 在Rt△ADE中, 根据勾股定理可求得DE, 即可得出∠FCE的正切值, 再在Rt△CEF中, 设EF=x,即可求出x, 从而得出CF=3x的长.
, 即可得出tanA, 在Rt△ADE中, 根据勾股定理可求得DE, 即可得出∠FCE的正切值, 再在Rt△CEF中, 设EF=x,即可求出x, 从而得出CF=3x的长.
解: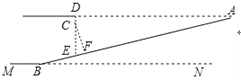
据题意得tanB=![]() ,
,
∵MN∥AD,
∴∠A=∠B,
∴tanA=![]() ,
,
∵DE⊥AD,
∴在Rt△ADE中,tanA=![]() ,
,
∵AD=9,
∴DE=3,
又∵DC=0.5,
∴CE=2.5,
∵CF⊥AB,
∴∠FCE+∠CEF=90°,
∵DE⊥AD,
∴∠A+∠CEF=90°,
∴∠A=∠FCE,
∴tan∠FCE=![]()
在Rt△CEF中,CE2=EF2+CF2
设EF=x,CF=3x(x>0),CE=2.5,
代入得(![]() )2=x2+(3x)2
)2=x2+(3x)2
解得x=![]() (如果前面没有“设x>0”,则此处应“x=±
(如果前面没有“设x>0”,则此处应“x=±![]() ,舍负”),
,舍负”),
∴CF=3x=![]() ≈2.3,
≈2.3,
∴该停车库限高2.3米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=![]() 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
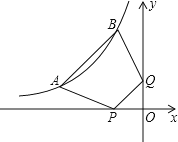
A.y=x B.y=x+1 C.y=x+2 D.y=x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)作图发现:
如图1,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向
为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .这时他发现
.这时他发现![]() 与
与![]() 的数量关系是 .
的数量关系是 .
(2)拓展探究:
如图2,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)解决问题
如图3,要测量池塘两岸相对的两点![]() ,
,![]() 的距离,已经测得
的距离,已经测得![]() ,
,![]() ,
,![]() 米,
米,![]() ,则
,则![]() 米.
米.
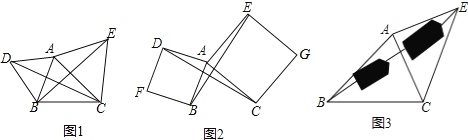
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
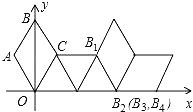
A. (1345,0) B. (1345.5,![]() ) C. (1345,
) C. (1345,![]() ) D. (1345.5,0)
) D. (1345.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,高
,高![]() 、
、![]() 相交于点
相交于点![]() ,
, ![]() ,且
,且![]() .
.
(1)求线段 ![]() 的长;
的长;
(2)动点 ![]() 从点
从点 ![]() 出发,沿线段
出发,沿线段 ![]() 以每秒 1 个单位长度的速度向终点
以每秒 1 个单位长度的速度向终点 ![]() 运动,动点
运动,动点 ![]() 从 点
从 点 ![]() 出发沿射线
出发沿射线![]() 以每秒 4 个单位长度的速度运动,
以每秒 4 个单位长度的速度运动,![]() 两点同时出发,当点
两点同时出发,当点 ![]() 到达
到达 ![]() 点时,
点时,![]() 两点同时停止运动.设点
两点同时停止运动.设点 ![]() 的运动时间为
的运动时间为 ![]() 秒,
秒,![]() 的面积为
的面积为 ![]() ,请用含
,请用含![]() 的式子表示
的式子表示 ![]() ,并直接写出相应的
,并直接写出相应的 ![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点 ![]() 是直线
是直线![]() 上的一点且
上的一点且 ![]() .是否存在
.是否存在![]() 值,使以点
值,使以点 ![]() 为顶 点的三角形与以点
为顶 点的三角形与以点 ![]() 为顶点的三角形全等?若存在,请直接写出符合条件的
为顶点的三角形全等?若存在,请直接写出符合条件的 ![]() 值; 若不存在,请说明理由.
值; 若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.

请根据图中信息解决下列问题:
(1)共有多少名同学参与问卷调查;
(2)补全条形统计图和扇形统计图;
(3)全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com