
【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
【答案】(1)购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.(2)有三种进货方案.方案一:甲种纪念品60件,乙种纪念品20件;方案二:甲种纪念品61件,乙种纪念品19件;方案三:甲种纪念品62件,乙种纪念品18件.(3)若全部销售完,方案一获利最大,最大利润是1800元.
【解析】分析:(1)设购进甲种纪念品每件价格为x元,乙种纪念币每件价格为y元,根据题意得出关于x和y的二元一次方程组,解方程组即可得出结论;
(2)设购进甲种纪念品a件,根据题意列出关于x的一元一次不等式,解不等式得出a的取值范围,即可得出结论;
(3)找出总利润关于购买甲种纪念品a件的函数关系式,由函数的增减性确定总利润取最值时a的值,从而得出结论.
详解:(1)设购进甲种纪念品每件需x元,购进乙种纪念品每件需y元.
由题意得:![]() ,
,
解得:![]()
答:购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.
(2)设购进甲种纪念品a(a≥60)件,则购进乙种纪念品(80﹣a)件.由题意得:
100a+50(80﹣a)≤7100
解得a≤62
又a≥60
所以a可取60、61、62.
即有三种进货方案.
方案一:甲种纪念品60件,乙种纪念品20件;
方案二:甲种纪念品61件,乙种纪念品19件;
方案三:甲种纪念品62件,乙种纪念品18件.
(3)设利润为W,则W=20a+30(80﹣a)=﹣10a+2400
所以W是a的一次函数,﹣10<0,W随a的增大而减小.
所以当a最小时,W最大.此时W=﹣10×60+2400=1800
答:若全部销售完,方案一获利最大,最大利润是1800元.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
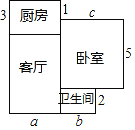
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=9,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米200元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米100元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
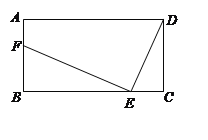
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若![]() ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C分别表示数﹣3、﹣1、2.
![]()
(1)A、B两点的距离AB=________,A、C两点的距离AC=________ ;
(2)通过观察,可以发现数轴上两点间距离与这两点表示的数的差的绝对值有一定关系,按照此关系,若点E表示的数为x,则AE=________ ;
(3)利用数轴直接写出|x﹣1|+|x+3|的最小值=________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,求甲巡逻艇的航向.
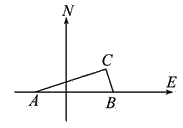
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…,![]() .
.
(1)计算P7÷P8的值;
(2)计算2P2019+P2020的值;
(3)猜想2Pn与Pn+1的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).
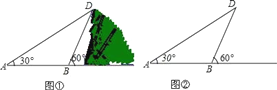
(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);
(2)山高DC是多少(结果保留根号形式)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com