练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】记：P1＝﹣2，P2＝（﹣2）×（﹣2），P3＝（﹣2）×（﹣2）×（﹣2），…，．

    （1）计算P7÷P8的值；

    （2）计算2P2019+P2020的值；

    （3）猜想2Pn与Pn+1的关系，并说明理由．

    【答案】（1）﹣；（2）0；（3）2Pn与Pn+1的关系：互为相反数的关系．

    【解析】

    （1）根据已知算式即可求解；

    （2）观察已知算式发现规律即可求值；

    （3）分两种情况讨论，当n为奇数和偶数时，n+1为偶数和奇数，进而可以说明．

    （1）∵P1＝﹣2＝（﹣2）1，

    P2＝（﹣2）×（﹣2）＝（﹣2）2，

    P3＝（﹣2）×（﹣2）×（﹣2）＝（﹣2）3，

    …，

    ＝（﹣2）n

    ∴P7÷P8的值为：（﹣2）7÷（﹣2）8＝﹣；

    （2）2P2019+P2020的值为：

    2（﹣2）2019+（﹣2）2020

    ＝﹣22020+22020

    ＝0；

    （3）2Pn与Pn+1的关系：互为相反数的关系．理由如下：

    2pn＝2（﹣2）n，

    pn+1＝（﹣2）n+1，

    当n为奇数时，n+1为偶数，

    ∴2pn＝2（﹣2）n＝﹣2n+1

    pn+1＝（﹣2）n+1＝2n+1

    ﹣2n+1与2n+1互为相反数；

    当n为偶数时，n+1为奇数，

    ∴2pn＝2（﹣2）n＝2n+1

    pn+1＝（﹣2）n+1＝﹣2n+1

    2n+1与﹣2n+1互为相反数；

    所以2Pn与Pn+1的关系：互为相反数的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，和是分别沿着边AB、AC翻折180°形成的．DC的延长线交AE于点O，交BE的延长线于点F．若，，则的度数为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】The coordinates of the three points A．B．C on the plane are (﹣5，﹣5)，(﹣2，﹣1)and(﹣1，﹣2)respectively，the triangle ABC is(　　)

    (英汉小词典：right直角的；isosceles等腰的；equilateral等边的；obtuse钝角的)

    A. a right trisngleB. an isosceles triangle

    C. an equilateral triangleD. an obtuse triangle

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市正在举行文化艺术节活动，一商店抓住商机，决定购进甲，乙两种艺术节纪念品．若购进甲种纪念品4件，乙种纪念品3件，需要550元，若购进甲种纪念品5件，乙种纪念品6件，需要800元．

    （1）求购进甲、乙两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共80件，其中甲种纪念品的数量不少于60件．考虑到资金周转，用于购买这80件纪念品的资金不能超过7100元，那么该商店共有几种进货方案7

    （3）若销售每件甲种纪含晶可获利润20元，每件乙种纪念品可获利润30元．在（2）中的各种进货方案中，若全部销售完，哪一种方案获利最大？最大利利润多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查，其中有这样一个问题：老师在课堂上放手让学生提问和表达（ ）

    A．从不 B．很少 C．有时 D．常常 E．总是

    答题的学生在这五个选项中只能选择一项．下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图．

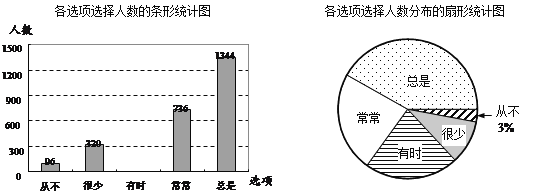
    根据以上信息，解答下列问题：

    （1）该区共有 名初二年级的学生参加了本次问卷调查；

    （2）请把这幅条形统计图补充完整；

    （3）在扇形统计图中，“总是”的圆心角为 ．（精确到度）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

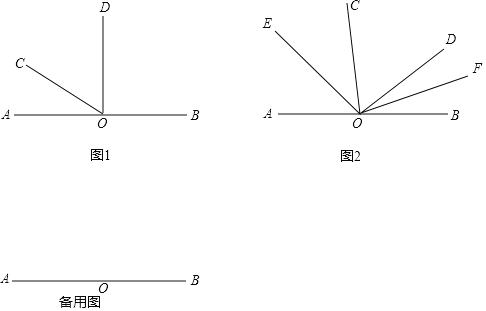
    【题目】已知：如图1，点O是直线AB上的一点．

    （1）如图1，当∠AOD是直角时，3∠AOC＝∠BOD，求∠COD的度数；

    （2）若∠COD保持在（1）中的大小不变，它绕着点O顺时针旋转（OD与OB重合即停止），如图2，OE、OF分别平分∠AOC、∠BOD，则在旋转过程中∠EOF的大小是否变化？若不变，求出∠EOF的大小；若改变，说明理由；

    （3）若∠COD从（1）中的位置开始，边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转（当其中一边与OB重合时都停止旋转），OM、ON分别平分∠BOC、∠BOD．

    求：①运动多少秒后，∠COD＝10°；

    ②运动多少秒后，∠COM＝∠BON．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线AB∥CD，∠A=∠C=100°，E、F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．

    （1）直线AD与BC有何位置关系？请说明理由.

    （2）求∠DBE的度数．

    （3）若把AD左右平行移动，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出此时∠ADB的度数；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，2），则点B2016的坐标为（　　）

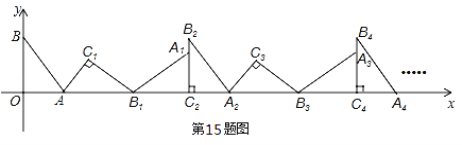
    A. (4032 ,2) B. (6048,2) C. (4032,0) D. (6048,0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.

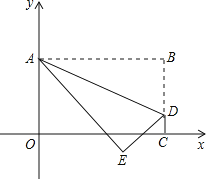
    (1)当m=3时,点B的坐标为 ,点E的坐标为 ；

    (2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.

    (3)如图,若点E的纵坐标为-1,且点(2,a)落在△ADE的内部,求a的取值范围.

    查看答案和解析>>

    同步练习册答案