
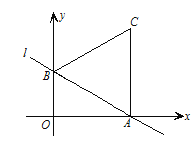
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
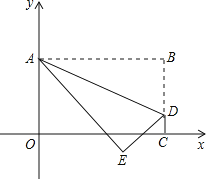
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
(3)如图,若点E的纵坐标为-1,且点(2![]() ,a)落在△ADE的内部,求a的取值范围.
,a)落在△ADE的内部,求a的取值范围.
【答案】(1)(3,4),(0,1);(2)能,m=![]() ;(3)1<a<2.
;(3)1<a<2.
【解析】
(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可;
(3)过点E作EF⊥AB于F,EF分别与 AD、OC交于点G、H,过点D作DP⊥EF于点P,首先利用勾股定理求得线段DP的长,从而求得线段BF的长,再利用△AFG∽△ABD得到比例线段求得线段FG的长,最后求得a的取值范围.
(1)点B的坐标为(3,4),
∵AB=BD=3,
∴△ABD是等腰直角三角形,
∴∠BAD=45°,
则∠DAE=∠BAD=45°,
则E在y轴上.
AE=AB=BD=3,
∴四边形ABDE是正方形,OE=1,
则点E的坐标为(0,1);
故答案为(3,4),(0,1);
(2)点E能恰好落在x轴上.理由如下:
∵四边形OABC为矩形,
∴BC=OA=4,∠AOC=∠DCE=90,
由折叠的性质可得:DE=BD=OACD=41=3,AE=AB=OC=m,
如图,假设点E恰好落在x轴上,在Rt△CDE中,由
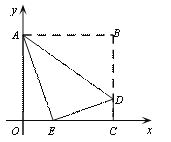
勾股定理可得EC=![]() =
=![]() =
=![]() ,
,
则有OE=OCCE=m![]() ,
,
在Rt△AOE中,OA2+OE2=AE2,
即![]() ,解得m=
,解得m=![]() ;
;
(3)如图,过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,过点D作DP⊥EF于点P,则EP=PH+EH=DC+EH=2,
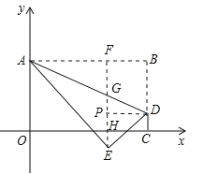
在Rt△PDE中,由勾股定理可得![]() ,
,
∴BF=DP=![]() ,
,
在Rt△AEF中,AF=ABBF=m![]() ,EF=5,AE=m
,EF=5,AE=m
∵AF2+EF2=AE2
∴(m![]() )2+52=m2,
)2+52=m2,
解得m=![]() ,
,
∴AB=![]() ,AF=
,AF=![]() ,E(
,E(![]() ,1)
,1)
∵∠AFG=∠ABD=90,∠FAG=∠BAD
∴△AFG∽△ABD
∴![]() ,即
,即![]() ,
,
解得FG=2,
∴EG=EFFG=3
∴点G的纵坐标为2,
∵点(![]() ,a)在直线x=
,a)在直线x=![]() 上,且点(
上,且点(![]() ,a)落在△ADE的内部,
,a)落在△ADE的内部,
∴此点必在EG上,
∴1<a<2,
故a的取值范围为1<a<2.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…,![]() .
.
(1)计算P7÷P8的值;
(2)计算2P2019+P2020的值;
(3)猜想2Pn与Pn+1的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).
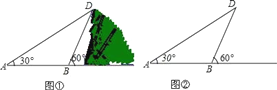
(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);
(2)山高DC是多少(结果保留根号形式)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 的解析式为
的解析式为![]() ,该直线与
,该直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以
,以![]() 为边在第一象限内作正△ABC.若点
为边在第一象限内作正△ABC.若点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有______(只填写正确结论的序号).
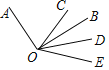
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
功率 | 使用寿命 | 价格 | |
普通白炽灯 |
|
|
|
优质节能灯 |
|
|
|
已知这两种灯的照明效果一样,小明家所在地的电价是每度![]() 元.(注:用电度数
元.(注:用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时),费用
时间(小时),费用![]() 灯的售价
灯的售价![]() 电费);如:若选用一盏普通白炽灯照明
电费);如:若选用一盏普通白炽灯照明![]() 小时,那么它的费用为
小时,那么它的费用为![]() (元),请解决以下问题:
(元),请解决以下问题:
(1)在白炽灯的使用寿命内,设照明时间为![]() 小时,请用含
小时,请用含![]() 的代数式分别表示用一盏白炽灯的费用
的代数式分别表示用一盏白炽灯的费用![]() ,(元)和一盏节能灯的费用
,(元)和一盏节能灯的费用![]() (元);
(元);
(2)在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?
(3)如果计划照明![]() 小时,购买哪一种灯更省钱?请你通过计算说明理由.
小时,购买哪一种灯更省钱?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com