【题目】如图，在平面直角坐标系
中，点
的坐标为(0，4)，线段
的位置如图所示，其中点
的坐标为(
，
)，点
的坐标为(3，
).
(1)将线段平移得到线段
，其中点的对应点为，点的对应点为点
.
①点平移到点的过程可以是：先向 平移 个单位长度，再向 平移 个单位长度；
②点的坐标为 .
(2)在(1)的条件下，若点
的坐标为(4，0)，连接
，画出图形并求
的面积.
长江作业本同步练习册系列答案科目：初中数学 来源： 题型：
【题目】已知：在
和
中，
，
，将如图摆放，使得
的两条边分别经过点
和点
．
（1）当将如图1摆放时，则
_________度．
（2）当将如图2摆放时，请求出
的度数，并说明理由．
（3）能否将摆放到某个位置时，使得
、
同时平分
和
？直接写出结论_______（填“能”或“不能”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如：某三角形三边长分别是5，6和8，因为
，所以这个三角形是常态三角形。
（1）若△ABC三边长分别是2，
和4，则此三角形_________常态三角形（填“是”或“不是”）；
（2）若Rt△ABC是常态三角形，则此三角形的三边长之比为__________________（请按从小到大排列）；
（3）如图，Rt△ABC中，∠ACB=90°，BC=6，点D为AB的中点，连接CD，若△BCD是常态三角形，求△ABC的面积。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD与矩形EFGH在直线l的同侧，边AD，EH在直线l上，且AD=5cm，EH=4cm，EF=3cm．保持正方形ABCD不动，将矩形EFGH沿直线l左右移动，连接BF，CG，则BF+CG的最小值为_____________cm
查看答案和解析>>
科目：初中数学 来源： 题型：
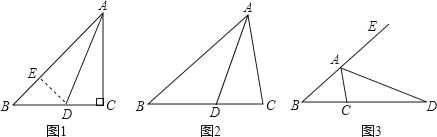
【题目】在△ABC中，∠ACB=2∠B，如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD．
（1）如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想：
（2）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y=﹣
图象上的点，并且y1＜0＜y2＜y3，则下列各式中正确的是（ ）
A．x1＜x2＜x3 B．x1＜x3＜x2
C．x2＜x1＜x3 D．x2＜x3＜x1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某电器商店计划从厂家购进
两种不同型号的电风扇，若购进8台
型和20台
型电风扇，需资金7600元，若购进4台型和15台型电风扇，需资金5300元.
（1）求型电风扇每台的进价各是多少元；
（2）该商店经理计划进这两种电风扇共50台，而可用于购买这两种电风扇的资金不超过12800元，根据市场调研，销售一台型电风扇可获利80元，销售一台型电风扇可获利120元.若两种电扇销售完时，所获得的利润不少于5000元.问有哪几种进货方案？哪种方案获得最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1、x2
（1）求实数k的取值范围。
（2）若方程两实根x1、x2满足x1+x2=﹣x1x2，求k的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
