练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为测山高，在点A处测得山顶D的仰角为30°，从点A向山的方向前进140米到达点B，在B处测得山顶D的仰角为60°（如图①）．

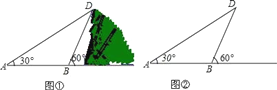
    （1）在所给的图②中尺规作图：过点D作DC⊥AB，交AB的延长线于点C（保留作图痕迹）；

    （2）山高DC是多少（结果保留根号形式）？

    【答案】（1）见解析；(2) 70.

    【解析】试题分析：（1）首先以点D为圆心，画弧交AB于两点，再分别以这两点为圆心，画弧，两弧交于一点，连接D与交点，即可求得作出垂线；

    （2）由在点A处测得山顶D的仰角为30°，可求得△ABD是等腰三角形，求得BD的长，继而求得答案．

    试题解析：解（1）如图所作DC为所求；

    （2）∵∠DBC=60°，∠DAB=30°，∴∠BDA=∠DAB=30°，∴DB=AB=140（米）．在Rt△DCB中，∠C=90°，sin∠DBC=，∴DC=140sin60°=70（米）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市正在举行文化艺术节活动，一商店抓住商机，决定购进甲，乙两种艺术节纪念品．若购进甲种纪念品4件，乙种纪念品3件，需要550元，若购进甲种纪念品5件，乙种纪念品6件，需要800元．

    （1）求购进甲、乙两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共80件，其中甲种纪念品的数量不少于60件．考虑到资金周转，用于购买这80件纪念品的资金不能超过7100元，那么该商店共有几种进货方案7

    （3）若销售每件甲种纪含晶可获利润20元，每件乙种纪念品可获利润30元．在（2）中的各种进货方案中，若全部销售完，哪一种方案获利最大？最大利利润多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，2），则点B2016的坐标为（　　）

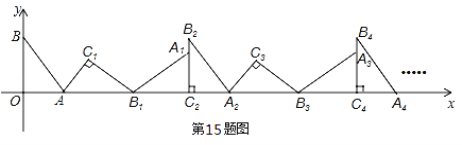
    A. (4032 ,2) B. (6048,2) C. (4032,0) D. (6048,0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为坐标原点．

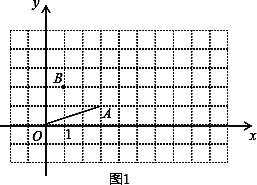
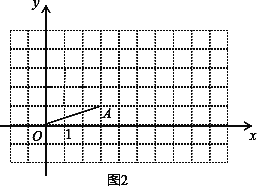
    （1）已知点A(3，1)，连结OA，作如下探究：

    探究一：平移线段OA，使点O落在点B.设点A落在点C,若点B的坐标为(1，2)，请在图1中作出BC，点C的坐标是_________；

    探究二：将线段OA绕点O逆时针旋转90°，设点A落在点D.则点D的坐标是_______.

    （2） 已知四点O(0，0)，A (a，b)， C，B(c，d)，顺次连结O，A，C，B．

    若所得到的四边形是正方形，请直接写出a，b，c，d应满足的关系式是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我市实施“城乡环境综合治理”期间，某校组织学生开展“走出校门，服务社会”的公益活动．八年级一班王浩根据本班同学参加这次活动的情况，制作了如下的统计图表：

    该班学生参加各项服务的频数、频率统计表：

    服务类别

    频数

    频率

    文明宣传员

    4

    0.08

    文明劝导员

    10

    义务小警卫

    8

    0.16

    环境小卫士

    0.32

    小小活雷锋

    12

    0.24

    请根据上面的统计图表，解答下列问题：

    （1）该班参加这次公益活动的学生共有 名；

    （2）请补全频数、频率统计表和频数分布直方图；

    （3）若八年级共有900名学生报名参加了这次公益活动，试估计参加文明劝导的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，反比例函数y＝的图象与一次函数y＝k(x－2)的图象交点为A(3，2)，B(x，y)．

    (1)求反比例函数与一次函数的解析式及B点坐标；

    (2)若C是y轴上的点，且满足△ABC的面积为10，求C点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.

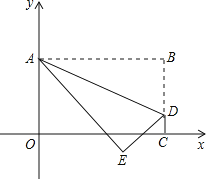
    (1)当m=3时,点B的坐标为 ,点E的坐标为 ；

    (2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.

    (3)如图,若点E的纵坐标为-1,且点(2,a)落在△ADE的内部,求a的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，□ABCD中，AB:BC=3:2，∠DCB=60°，点E在AB上，BE=2AE，点F为BC的中点，DP⊥AF，DQ⊥CE，则DP:DQ=（ ）

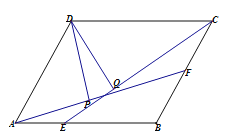
    A.3:4B.1:1C.：D.3：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ADE+∠BCF=180°，BE平分∠ABC，∠ABC=2∠E.

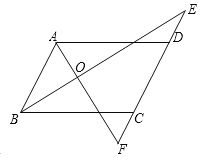
    （1）AD与BC平行吗？请说明理由；

    （2）AB与EF的位置关系如何？为什么？

    （3）若AF平分∠BAD，试说明：

    ①∠BAD=2∠F；②∠E+∠F=90°.

    注：本题第（1）、（2）小题在下面的解答过程的空格内填写理由或数学式；第（3）小题要写出解题过程.

    解：（1）AD∥BC，理由如下：

    ∵∠ADE+∠ADF=180°，（平角的定义）

    ∠ADE+∠BCF=180°，（已知）

    ∴∠ADF=∠______， （____________________________）

    ∴ AD∥BC （____________________________）

    （2）AB与EF的位置关系是：_______________.

    ∵BE平分∠ABC， （已知）

    ∴∠ABE=∠ABC. （角平分线的定义）

    又∵∠ABC=2∠E, （已知），

    即∠E=∠ABC,

    ∴∠E=∠_____. （_____________________________）

    ∴ ______∥_____. （_____________________________）

    查看答案和解析>>

    同步练习册答案