
【题目】在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
功率 | 使用寿命 | 价格 | |
普通白炽灯 |
|
|
|
优质节能灯 |
|
|
|
已知这两种灯的照明效果一样,小明家所在地的电价是每度![]() 元.(注:用电度数
元.(注:用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时),费用
时间(小时),费用![]() 灯的售价
灯的售价![]() 电费);如:若选用一盏普通白炽灯照明
电费);如:若选用一盏普通白炽灯照明![]() 小时,那么它的费用为
小时,那么它的费用为![]() (元),请解决以下问题:
(元),请解决以下问题:
(1)在白炽灯的使用寿命内,设照明时间为![]() 小时,请用含
小时,请用含![]() 的代数式分别表示用一盏白炽灯的费用
的代数式分别表示用一盏白炽灯的费用![]() ,(元)和一盏节能灯的费用
,(元)和一盏节能灯的费用![]() (元);
(元);
(2)在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?
(3)如果计划照明![]() 小时,购买哪一种灯更省钱?请你通过计算说明理由.
小时,购买哪一种灯更省钱?请你通过计算说明理由.
【答案】(1)![]() ;
;![]() ;(2)照明800小时时,使用这两种灯的费用相等;(3)购买节能灯更省钱,理由见解析.
;(2)照明800小时时,使用这两种灯的费用相等;(3)购买节能灯更省钱,理由见解析.
【解析】
(1)先根据“用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时)”求出两种灯的用电度数,再根据“费用
时间(小时)”求出两种灯的用电度数,再根据“费用![]() 灯的售价
灯的售价![]() 电费”列出等式即可;
电费”列出等式即可;
(2)令题(1)中的![]() 可得一个关于x的一元一次方程,求解即可;
可得一个关于x的一元一次方程,求解即可;
(3)根据照明4000小时,分别求出两种灯的费用,再进行大小比较即可.
(1)由题意得![]()
一盏白炽灯的用电度数为![]() 度,一盏节能灯的用电度数为
度,一盏节能灯的用电度数为![]() 度
度
则根据费用公式得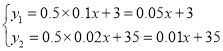
故答案为:![]() ;
;![]() ;
;
(2)由题意,令![]() 得
得![]()
解得![]()
故照明800小时时,使用这两种灯的费用相等;
(3)购买节能灯更省钱,理由如下:
当照明时间为4000小时时,若用白炽灯,需购买2盏
则其费用为![]() (元)
(元)
若用节能灯,只需购买1盏
则其费用为![]() (元)
(元)
因![]()
故购买节能灯更省钱.


科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题:

(1)该班参加这次公益活动的学生共有 名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
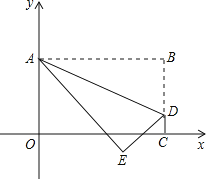
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
(3)如图,若点E的纵坐标为-1,且点(2![]() ,a)落在△ADE的内部,求a的取值范围.
,a)落在△ADE的内部,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长为1,宽为a的矩形纸片(![]() ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )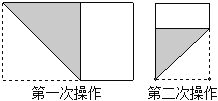
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,AB:BC=3:2,∠DCB=60°,点E在AB上,BE=2AE,点F为BC的中点,DP⊥AF,DQ⊥CE,则DP:DQ=( )
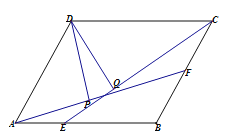
A.3:4B.1:1C.![]() :
:![]() D.3:
D.3:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
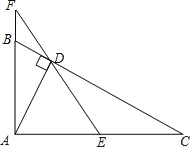
【题目】如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com